题目内容
(本题满分15分)
已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1相交于M、N两点.
(1).求实数k的取值范围
(2).求证: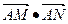 为定值
为定值
(3).若O为坐标原点,且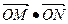 =12,求直线l的方程
=12,求直线l的方程
已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1相交于M、N两点.
(1).求实数k的取值范围
(2).求证:
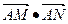 为定值
为定值(3).若O为坐标原点,且
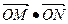 =12,求直线l的方程
=12,求直线l的方程解:(1).法一:直线l过点A(0,1),且斜率为k,则直线l的方程为y="kx+1 " 2分
将其代入圆C方程得: (1+k2)x2-4(1+k)x+7=0,由题意:△=[-4(1+k)]2-28(1+k2)>0得
 ……………… 5分
……………… 5分
法二:用直线和圆相交,圆心至直线的距离小于半径处理亦可
(2).证明:法一:设过A点的圆切线为AT,T为切点,则AT2=AM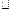 AN
AN
而AT2=(0-2)2+(1-3)2="7 " ……………… 7分
 ……………… 10分
……………… 10分
法二:用直线和圆方程联立计算证明亦可
(3).设M(x1,y1),N(x2,y2)由(1)知
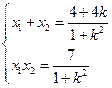 ……………… 12分
……………… 12分
 ………………14分
………………14分
k=1符合范围约束,故l:y="x+1 " ……………… 15分
将其代入圆C方程得: (1+k2)x2-4(1+k)x+7=0,由题意:△=[-4(1+k)]2-28(1+k2)>0得
 ……………… 5分
……………… 5分法二:用直线和圆相交,圆心至直线的距离小于半径处理亦可
(2).证明:法一:设过A点的圆切线为AT,T为切点,则AT2=AM
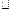 AN
AN而AT2=(0-2)2+(1-3)2="7 " ……………… 7分
 ……………… 10分
……………… 10分法二:用直线和圆方程联立计算证明亦可
(3).设M(x1,y1),N(x2,y2)由(1)知
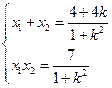 ……………… 12分
……………… 12分 ………………14分
………………14分k=1符合范围约束,故l:y="x+1 " ……………… 15分
略

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 2个小题,第1小题满分6分,第2小题满分8分.
2个小题,第1小题满分6分,第2小题满分8分. 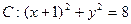 .
. 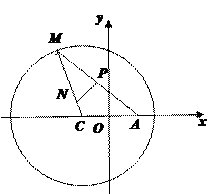
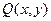 是圆C上一点,求
是圆C上一点,求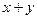 的取值范围;
的取值范围;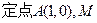 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足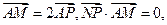 求
求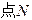 的轨迹的内接矩形的
的轨迹的内接矩形的 最大面积.
最大面积.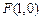 ,
,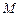 点在
点在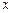 轴的负半轴上,点
轴的负半轴上,点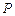 在
在
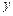 轴上,且
轴上,且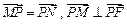 .
. 动时,求点
动时,求点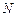 的轨迹
的轨迹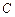 的方程;
的方程;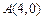 ,是否存在垂直
,是否存在垂直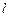 被以
被以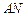 为直径的圆截得的弦长恒为定值?若存在,求出直线
为直径的圆截得的弦长恒为定值?若存在,求出直线
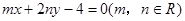 始终平分圆
始终平分圆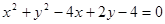 的周长,则
的周长,则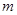 、
、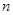 的关系是 ( )
的关系是 ( )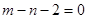
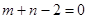

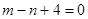
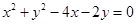 内的一点,则过点M的最短弦
内的一点,则过点M的最短弦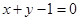 B
B 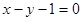 C
C 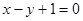 D
D 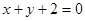
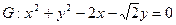 经过椭圆
经过椭圆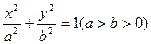 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点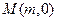 作倾斜角为
作倾斜角为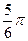 的直线
的直线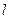 交椭圆于C、D两点.
交椭圆于C、D两点.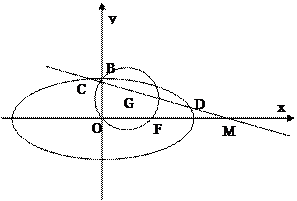
 恰在以线段CD为直径
恰在以线段CD为直径 部,求实数
部,求实数 范围.
范围.
 作圆
作圆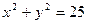 的两条切线,切点为
的两条切线,切点为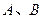 ,则点
,则点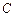 到直线
到直线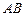 的
的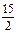
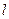 过点
过点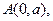 斜率为1,圆
斜率为1,圆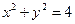 上恰有3个点到
上恰有3个点到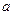 的值为××××××.
的值为××××××.