题目内容
已知椭圆E: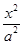 +
+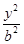 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
A.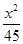 +
+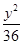 =1 B.
=1 B.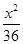 +
+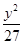 =1
=1
C.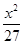 +
+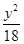 =1 D.
=1 D.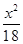 +
+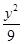 =1
=1
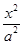 +
+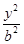 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).A.
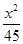 +
+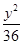 =1 B.
=1 B.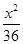 +
+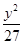 =1
=1C.
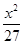 +
+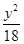 =1 D.
=1 D.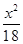 +
+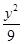 =1
=1D
设A(x1,y1)、B(x2,y2),所以 运用点差法,
运用点差法,
所以直线AB的斜率为k=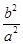 ,
,
设直线方程为y=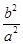 (x-3),
(x-3),
联立直线与椭圆的方程得(a2+b2)x2-6b2x+9b2-a4=0,
所以x1+x2= =2,
=2,
又因为a2-b2=9,解得b2=9,a2=18.
∴椭圆的方程为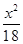 +
+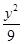 =1.
=1.
 运用点差法,
运用点差法,所以直线AB的斜率为k=
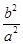 ,
,设直线方程为y=
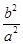 (x-3),
(x-3),联立直线与椭圆的方程得(a2+b2)x2-6b2x+9b2-a4=0,
所以x1+x2=
 =2,
=2,又因为a2-b2=9,解得b2=9,a2=18.
∴椭圆的方程为
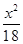 +
+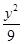 =1.
=1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +
+ =1(a>b>0).
=1(a>b>0). ,求椭圆的标准方程.
,求椭圆的标准方程.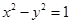 的焦点与椭圆
的焦点与椭圆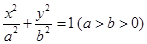 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为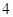 ,
,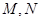 是椭圆上的的动点.
是椭圆上的的动点.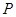 满足:
满足: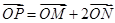 ,直线
,直线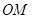 与
与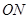 的斜率之积为
的斜率之积为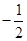 ,求证:存在定点
,求证:存在定点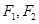 ,
,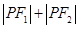 为定值,并求出
为定值,并求出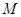 在第一象限,且点
在第一象限,且点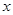 轴的射影为
轴的射影为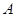 ,连接
,连接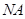 并延长交椭圆于
并延长交椭圆于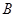 ,求证:以
,求证:以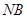 为直径的圆经过点
为直径的圆经过点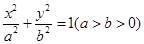 的离心率为
的离心率为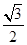 ,则双曲线
,则双曲线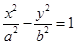 的渐近线方程是________
的渐近线方程是________ 上有一点P到左焦点的距离是4,则点p到右焦点的距离是( ).
上有一点P到左焦点的距离是4,则点p到右焦点的距离是( ).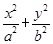 =1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2=
=1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2=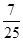 ,则直线CD的斜率为________.
,则直线CD的斜率为________.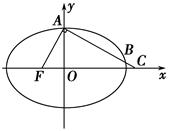
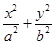 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.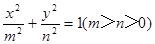 和双曲线
和双曲线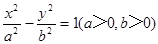 有相同的焦点
有相同的焦点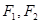 ,
,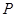 是两曲线的一个交点,则
是两曲线的一个交点,则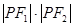 的值是( )
的值是( )
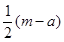


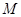 为椭圆
为椭圆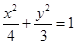 上一点,
上一点,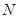 为椭圆长轴上一点,
为椭圆长轴上一点,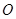 为坐标原点.
为坐标原点.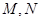 ,使得
,使得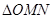 为等边三角形;
为等边三角形;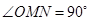 ;
;