题目内容
如图，△ABC的角平分线AD的延长线交它的外接圆于点E。
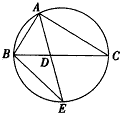
（1）证明：△ABE∽△ADC；
（2）若△ABC的面积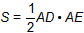
，求∠BAC的大小。
（2）若△ABC的面积
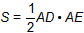，求∠BAC的大小。解：（1）由已知△ABC的角平分线为AD，
可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角，
所以∠AEB=∠ACD
故△ABE∽△ADC；
（2）因为△ABE∽△ADC，
所以
即AB·AC=AD·AE
又S=
且
故AB·ACsin∠BAC=AD·AE
则sin∠BAC=1，
又∠BAC为三角形内角，
所以∠BAC=90°。
可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角，
所以∠AEB=∠ACD
故△ABE∽△ADC；
（2）因为△ABE∽△ADC，
所以
即AB·AC=AD·AE
又S=
且
故AB·ACsin∠BAC=AD·AE
则sin∠BAC=1，
又∠BAC为三角形内角，
所以∠BAC=90°。
练习册系列答案
相关题目
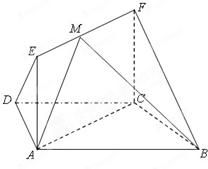如图，在梯形ABCD中，AB∥C，AD=DC=CB=1，∠ABC═60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
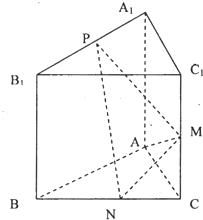（2012•自贡三模）如图所示，己知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M，N分别是CC1，BC的中点，P点在A1B1上，且满足
如图正三棱锥ABC-A1B1C1中，底面边长为a，侧棱长为
，若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
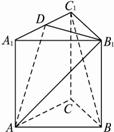
的侧棱与底面垂直，
，MN分别是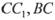
的中点，P点在
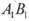上，且满足
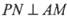
取何值时，直线PN与平面ABC所成的角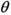
最大？并求出该最大角的正切值；