题目内容
 (2012•自贡三模)如图所示,己知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,P点在A1B1上,且满足
(2012•自贡三模)如图所示,己知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,P点在A1B1上,且满足| A1P |
| A1B1 |
(I)证明:PN⊥AM;
(II)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求出该最大角的正切值;
(III)在(II)条件下求P到平而AMN的距离.
分析:(Ⅰ) 以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,分别求出
与
的坐标,要证PN⊥AM,只需求证它们的数量积为零即可;
(II)设出平面ABC的一个法向量,表达出sinθ,利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正切值;
(III)求出平面AMN的法向取
=(1,-1,2),
=(
,0,1),利用d=
可得结论.
| PN |
| AM |
(II)设出平面ABC的一个法向量,表达出sinθ,利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正切值;
(III)求出平面AMN的法向取
| m |
| AP |
| 1 |
| 2 |
|
| ||||
|
|
解答: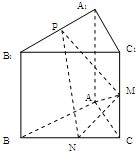 (Ⅰ) 证明:以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz
(Ⅰ) 证明:以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz
则P(λ,0,1),N(
,
,0),M(0,1,
)
∴
=(
-λ,
,-1),
=(0,1,
)
从而
•
=
-
=0,∴PN⊥AM;
(Ⅱ)解:平面ABC的一个法向量为
=(0,0,1),
则sinθ=|cos<
,
>|=
=
而θ∈[0,
],当θ最大时,sinθ最大,tanθ最大,
故λ=
时,sinθ取到最大值
时,tanθ=2.
(Ⅲ)解:设平面AMN的法向量为
=(x,y,z)
由
•
=0,
•
=0,得
,∴可取
=(1,-1,2)
∵
=(
,0,1)
∴d=
=
.
 (Ⅰ) 证明:以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz
(Ⅰ) 证明:以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz则P(λ,0,1),N(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| PN |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
从而
| PN |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)解:平面ABC的一个法向量为
| n |
则sinθ=|cos<
| PN |
| n |
|
| ||||
|
|
| 1 | ||||||
|
而θ∈[0,
| π |
| 2 |
故λ=
| 1 |
| 2 |
2
| ||
| 5 |
(Ⅲ)解:设平面AMN的法向量为
| m |
由
| m |
| AN |
| m |
| AM |
|
| m |
∵
| AP |
| 1 |
| 2 |
∴d=
|
| ||||
|
|
5
| ||
| 12 |
点评:利用向量知识解决立体几何问题的优点在于用代数化的方法解决立体几何,解题的关键在于用坐标表示空间向量,熟练掌握向量夹角公式

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目