题目内容
12．设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[0，2]时，f（x）=（$\sqrt{2}$）x-1，若关于x的方程f（x）-loga（x+2）=0（a＞0且a≠1）在区间（-2，6）内恰有4个不等的实数根，则实数a的取值范围是（ ）| A． | （$\frac{1}{4}$，1） | B． | （1，4） | C． | （1，8） | D． | （8，+∞） |
分析 由题意，讨论0＜a＜1时，当0＜a＜1时，-2＜x＜0时，y=f（x）和y=loga（x+2）只有一个交点；故a＞1．关于x的方程f（x）-loga（x+2）=0（a＞1），在区间（-2，6）内恰有四个不同实根可化为函数f（x）与函数y=loga（x+2）有四个不同的交点，作出函数f（x）与函数y=loga（x+2）的图象，由图象解出答案．
解答 
解：由f（x）是定义在R上的偶函数，
且f（2+x）=f（2-x），
即为f（x+4）=f（-x）=f（x），
则f（x）为周期为4的函数．
当x∈[0，2]时，f（x）=（$\sqrt{2}$）x-1，
可得x∈[-2，0]时，f（x）=f（-x）=（$\sqrt{2}$）-x-1，
又∵f（x）=loga（x+2）（a＞0且a≠1），
当0＜a＜1时，-2＜x＜0时，y=f（x）和y=loga（x+2）只有一个交点；
在0＜x＜6时，f（x）＞0，loga（x+2）＜0，则没有交点，
故a＞1，作出它们在区间（-2，6）内图象如右图：
当x=6时，f（6）=f（2）=1，loga（6+2）=1，解得a=8，
由于-2＜x＜6，即有a＞8，
y=f（x）和y=loga（x+2）有四个交点．
故选：D．
点评 本题考查了方程的根与函数的零点之间的关系，同时考查了数形结合的数学思想应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
2．下列各函数中，最小值为2的是（ ）
| A． | $y=x+\frac{1}{x}$，x≠0且x∈R | B． | $y=\frac{sinx}{2}+\frac{2}{sinx}$，x∈（0，π） | ||
| C． | $y=\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$，x∈R | D． | y=ex+e-x，x∈R |
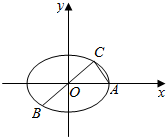已知A，B，C是椭圆M：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$上的不同三点，其中点A的坐标为（2$\sqrt{3}$，0），BC过椭圆的中心，点C在第一象限，且满足∠BAC=90°，|BC|=2|AC|．
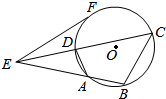已知四边形ABCD内接于⊙O，AD：BC=1：2，BA、CD的延长线交于点E，且EF切⊙O于F．
2．设函数f（x）=（x-2）lnx-ax+1，若存在唯一的整数x0，使得f（x0）＜0，则a的取值范围是（ ）
| A． | （0，$\frac{1+ln3}{3}$） | B． | （$\frac{1}{2}$，$\frac{1+ln3}{3}$] | C． | （$\frac{1+ln3}{3}$，1） | D． | [$\frac{1+ln3}{3}$，1） |