题目内容
2.下列各函数中,最小值为2的是( )| A. | $y=x+\frac{1}{x}$,x≠0且x∈R | B. | $y=\frac{sinx}{2}+\frac{2}{sinx}$,x∈(0,π) | ||
| C. | $y=\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$,x∈R | D. | y=ex+e-x,x∈R |
分析 根据基本不等式的性质分别对各个选项进行判断即可.
解答 解:对于A:x可能是负数;
对于B:若“=”成立,需sin2x=4,不可能取到;
对于C:若“=”成立,需x2+2=1,不可能取到;
对于D:y=ex+$\frac{1}{{e}^{x}}$≥2$\sqrt{{e}^{x}•\frac{1}{{e}^{x}}}$=2,
当且仅当ex=1时“=”成立,
故选:D.
点评 本题考查了基本不等式的性质,注意满足取“=”的条件,本题是一道基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
7.数列{an}中,an=$\frac{4n-π}{2n-11}$,则该数列最大项是( )
| A. | a1 | B. | a5 | C. | a6 | D. | a7 |
11.“$\frac{1}{x}≥1$”是“2x-1≤1”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[0,2]时,f(x)=($\sqrt{2}$)x-1,若关于x的方程f(x)-loga(x+2)=0(a>0且a≠1)在区间(-2,6)内恰有4个不等的实数根,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
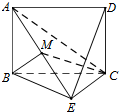 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点. 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])