题目内容
已知函数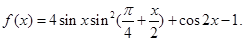
(1)设 >0为常数,若
>0为常数,若 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(2)设集合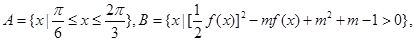 若A
若A B恒成立,求实数
B恒成立,求实数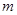 的取值范围.
的取值范围.
(1)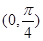 ;(2)
;(2)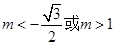
解析试题分析:解题思路:利用二倍角公式的变形将 化成
化成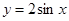 的形式,利用
的形式,利用 求解;(2)由题意得知,该问是不等式恒成立问题,将
求解;(2)由题意得知,该问是不等式恒成立问题,将 化成关于
化成关于 的一元二次函数求最值问题.规律总结:1.三角恒等变换要正确选用公式及其变形;2.求关于
的一元二次函数求最值问题.规律总结:1.三角恒等变换要正确选用公式及其变形;2.求关于 的一元二次函数的值域或最值时,要注意三角函数的有界性.
的一元二次函数的值域或最值时,要注意三角函数的有界性.
试题解析:⑴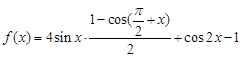
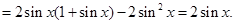
 是增函数,
是增函数,
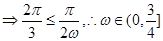
(2)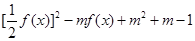
=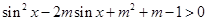
因为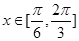 ,设
,设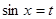 ,则
,则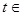 [
[ ,1]
,1]
上式化为
由题意,上式在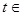 [
[ ,1]上恒成立.
,1]上恒成立.
记 ,
,
这是一条开口向上抛物线,
则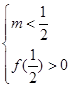 或
或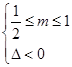 或
或
解得: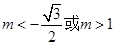 .
.
考点:1.平面向量的数量积;2.一元二次函数的最值;3.不等式恒成立.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 中,
中, ,
,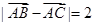 ,点
,点 是线段
是线段 (含端点)上的一点,且
(含端点)上的一点,且 ,则
,则 的取值范围是 .
的取值范围是 .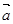 =(
=(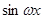 ,
,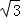
 =(
=(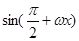 ),(ω>0),
),(ω>0),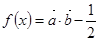 且
且 的最小正周期是
的最小正周期是 .
. 的值;
的值;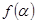 =
=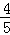 (
(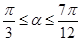 ),求
),求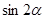 值;
值;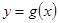 与
与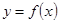 的图象关于直线
的图象关于直线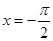 对称,且方程
对称,且方程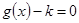 在区间
在区间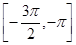 上有解,求
上有解,求 的取值范围.
的取值范围.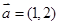 ,
, ,当
,当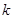 为何值时,
为何值时,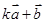 与
与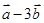 垂直?(2)
垂直?(2)  与
与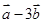 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向? =(cos
=(cos ,cos(
,cos( ),
), =(
=( ,sin
,sin
 的值;
的值; ,求
,求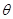 ;
; ,求证:
,求证: .
.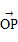 =
=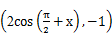 ,
,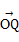 =
=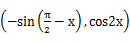 ,定义函数f(x)=
,定义函数f(x)=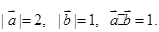
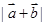 的值; (2)若
的值; (2)若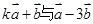 垂直,求
垂直,求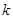 的值.
的值. 是函数
是函数 ,
, )一个周期内图象上的两点,函数
)一个周期内图象上的两点,函数 的图象与
的图象与 轴交于点
轴交于点 ,满足
,满足 .
. 在区间
在区间 内的零点.
内的零点. =
= (
(  +
+ ),
), =
=
 ,则
,则 =________.
=________.