题目内容
【题目】已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
【答案】(1)![]() ;(2)存在
;(2)存在![]()
【解析】
试题分析:(1)直线方程![]() 为:
为:![]()
![]()

![]()
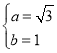
![]() 椭圆方程为
椭圆方程为 ![]() ;(2)假若存在这样的
;(2)假若存在这样的![]() 值,由
值,由
![]()
![]()
![]() .
.
![]()
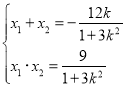
![]()
![]() .要使以
.要使以![]() 为直径的圆过点
为直径的圆过点![]()
![]() 当且仅当
当且仅当![]() 时
时![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 存在
存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
试题解析:(1)直线方程![]() 为:
为:![]() .
.
依题意 解得
解得 
∴ 椭圆方程为 ![]()
(2)假若存在这样的![]() 值,由
值,由 得
得![]()
![]() .
.
![]()
![]() . ①
. ①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则 ②
②
而![]() .
.
要使以![]() 为直径的圆过点
为直径的圆过点![]() ,当且仅当
,当且仅当![]() 时,则
时,则![]() ,即
,即![]() .
.
![]()
![]() . ③
. ③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某班主任对全班50名学生作了一次调查,所得数据如表:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 18 | 9 | 27 |
不喜欢玩电脑游戏 | 8 | 15 | 23 |
总计 | 26 | 24 | 50 |
由表中数据计算得到K2的观测值k≈5.059,于是________(填“能”或“不能”)在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
【题目】为了判断高中三年级学生选修文理科是否与性别有关,现随机抽取50名学生,得到2×2列联表:
理科 | 文科 | 总计 | |
男 | 13 | 10 | 23 |
女 | 7 | 20 | 27 |
总计 | 20 | 30 | 50 |
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2≈4.844,则认为选修文理科与性别有关系出错的可能性约为________.