题目内容
在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x-b)>0的解集是(2,3),则a+b的值为( )
| A、1 | B、2 | C、4 | D、8 |
分析:根据定义,利用一元二次不等式的解法求不等式的解集.
解答:解:∵x?y=x(1-y),
∴(x-a)?(x-b)>0得
(x-a)[1-(x-b)]>0,
即(x-a)(x-b-1)<0,
∵不等式(x-a)?(x-b)>0的解集是(2,3),
∴x=2,和x=3是方程(x-a)(x-b-1)=0的根,
即x1=a或x2=1+b,
∴x1+x2=a+b+1=2+3,
∴a+b=4,
故选:C.
∴(x-a)?(x-b)>0得
(x-a)[1-(x-b)]>0,
即(x-a)(x-b-1)<0,
∵不等式(x-a)?(x-b)>0的解集是(2,3),
∴x=2,和x=3是方程(x-a)(x-b-1)=0的根,
即x1=a或x2=1+b,
∴x1+x2=a+b+1=2+3,
∴a+b=4,
故选:C.
点评:本题主要考查一元二次不等式的解法,利用新定义列出不等式是解决本题的关键.

练习册系列答案
相关题目
 :x
:x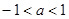 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.