题目内容
一数列{an}的前n项的平均数为n.(1)求数列{an}的通项公式;
(2)设
 ,证明数列{bn}是递增数列;
,证明数列{bn}是递增数列;(3)设
 ,是否存在最大的数M?当x≤M时,对于一切非零自然数n,都有f(x)≤0.
,是否存在最大的数M?当x≤M时,对于一切非零自然数n,都有f(x)≤0.
【答案】分析:(1)利用平均数的意义和当n=1时,a1=S1=1;当n≥2时,an=Sn-Sn-1即可得出;
(2)作差bn+1-bn,证明其大于0即可;
(3)利用(2)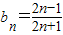 递增,因此有最小值
递增,因此有最小值 .解出
.解出 ,即可知道是否存在最大的数M.
,即可知道是否存在最大的数M.
解答:解:(1)由题意可得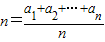 ,∴
,∴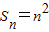 ,
,
当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
当n=1时也成立.故an=2n-1.
(2)作差bn+1-bn= =
=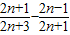 =
= =
= ,
,
∴bn+1>bn对于任意正整数n都成立,因此数列{bn}是递增数列.
(3)∵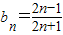 递增,∴有最小值
递增,∴有最小值 ,
,
∴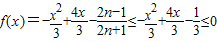 ,解得x2-4x+1≥0,
,解得x2-4x+1≥0,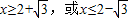 .
.
所以M= .
.
存在最大的数M= ,当x≤M时,对于一切非零自然数n,都有f(x)≤0.
,当x≤M时,对于一切非零自然数n,都有f(x)≤0.
点评:熟练掌握数列的通项公式与其前n项和之间的关系、作差法比较数的大小、一元二次不等式的解法及其转化法等是解题的关键.
(2)作差bn+1-bn,证明其大于0即可;
(3)利用(2)
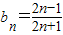 递增,因此有最小值
递增,因此有最小值 .解出
.解出 ,即可知道是否存在最大的数M.
,即可知道是否存在最大的数M.解答:解:(1)由题意可得
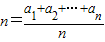 ,∴
,∴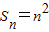 ,
,当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
当n=1时也成立.故an=2n-1.
(2)作差bn+1-bn=
 =
=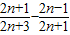 =
= =
= ,
,∴bn+1>bn对于任意正整数n都成立,因此数列{bn}是递增数列.
(3)∵
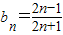 递增,∴有最小值
递增,∴有最小值 ,
,∴
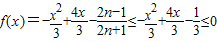 ,解得x2-4x+1≥0,
,解得x2-4x+1≥0,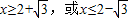 .
.所以M=
 .
.存在最大的数M=
 ,当x≤M时,对于一切非零自然数n,都有f(x)≤0.
,当x≤M时,对于一切非零自然数n,都有f(x)≤0.点评:熟练掌握数列的通项公式与其前n项和之间的关系、作差法比较数的大小、一元二次不等式的解法及其转化法等是解题的关键.

练习册系列答案
相关题目