题目内容
 (2012•唐山二模)选修4-1:几何证明选讲
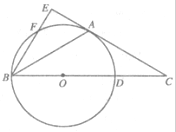
(2012•唐山二模)选修4-1:几何证明选讲如图,在△ABC中,BC边上的点D满足BD=2DC,以BD为直径作圆O恰与CA相切于点A,过点B作BE⊥CA于点E,BE交圆D于点F.
(I)求∠ABC的度数:
( II)求证:BD=4EF.
分析:(Ⅰ)连接OA、AD.由AC是圆O的切线,OA=OB,知OA⊥AC,∠OAB=∠OBA=∠DAC,由AD是Rt△OAC斜边上的中线,知AD=OD=DC=OA,由△AOD是等边三角形,能求出∠ABC的度数.
(Ⅱ)由(Ⅰ)可知,在Rt△AEB中,∠EAB=∠ADB=60°,由EA=
AB=
×
BD=
BD,知EB=
AB=
×
BD=
BD,由切割线定理,得EA2=EF×EB,由此能够证明BD=4EF.
(Ⅱ)由(Ⅰ)可知,在Rt△AEB中,∠EAB=∠ADB=60°,由EA=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
解答:解:(Ⅰ)连接OA、AD.
∵AC是圆O的切线,OA=OB,
∴OA⊥AC,∠OAB=∠OBA=∠DAC,…(2分)
又AD是Rt△OAC斜边上的中线,
∴AD=OD=DC=OA,
∴△AOD是等边三角形,∴∠AOD=60°,
故∠ABC=
∠AOD=30°.…(5分)
(Ⅱ)由(Ⅰ)可知,
在Rt△AEB中,∠EAB=∠ADB=60°,
∴EA=
AB=
×
BD=
BD,
EB=
AB=
×
BD=
BD,…(7分)
由切割线定理,得EA2=EF×EB,
∴
BD2=EF×
BD,
∴BD=4EF.…(10分)
∵AC是圆O的切线,OA=OB,
∴OA⊥AC,∠OAB=∠OBA=∠DAC,…(2分)
又AD是Rt△OAC斜边上的中线,
∴AD=OD=DC=OA,
∴△AOD是等边三角形,∴∠AOD=60°,
故∠ABC=
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)可知,
在Rt△AEB中,∠EAB=∠ADB=60°,
∴EA=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
EB=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
由切割线定理,得EA2=EF×EB,
∴
| 3 |
| 16 |
| 3 |
| 4 |
∴BD=4EF.…(10分)
点评:本题考查弦切角、与圆有关的比例线段的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
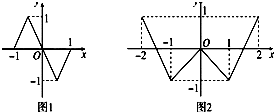 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )