题目内容
1.设等比数列{an}的各项均为正数,若$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{2}$=$\frac{2}{{a}_{1}}$+$\frac{2}{{a}_{2}}$,$\frac{{a}_{3}}{4}$+$\frac{{a}_{4}}{4}$=$\frac{4}{{a}_{3}}$+$\frac{4}{{a}_{4}}$,则a1a5=( )| A. | 24$\sqrt{2}$ | B. | 8 | C. | 8$\sqrt{2}$ | D. | 16 |
分析 化简整理利用等比数列的通项公式即可得出.
解答 解:∵$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{2}$=$\frac{2}{{a}_{1}}$+$\frac{2}{{a}_{2}}$,
∴$\frac{{a}_{1}+{a}_{2}}{2}=\frac{2({a}_{1}+{a}_{2})}{{a}_{1}{a}_{2}}$,
∵等比数列{an}的各项均为正数,
∴a1a2=4,
同理可得:a3a4=16.
∴q4=4,解得$q=\sqrt{2}$,${a}_{1}^{2}=\frac{4}{q}$.
则a1a5=${a}_{1}^{2}•{q}^{4}$=4q3=8$\sqrt{2}$.
故选:C.
点评 本题考查了等比数列的通项公式,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
下表是降耗技术改造后生产甲产品过程中记录的产量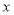 (吨)与相应的生产能耗
(吨)与相应的生产能耗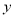 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出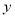 关于
关于 的线性回归方程
的线性回归方程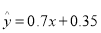 ,那么表中
,那么表中 的值为?( )
的值为?( )

A.4 B.3.5 C.3 D.4.5
12.将7个人(含甲、乙)分成三个组,一组3人,另两组各2人,则甲、乙分在同一组的概率是( )
| A. | $\frac{5}{21}$ | B. | $\frac{5}{42}$ | C. | $\frac{8}{21}$ | D. | $\frac{4}{21}$ |
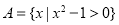 ,
, ,则
,则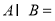 ( )
( ) B.
B. C.
C.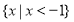 D.
D.