题目内容
5.设非负实数x,y满足$\left\{\begin{array}{l}{3x-y≥0}\\{x+3y+m≤0}\end{array}\right.$(m<0),则不等式所表示的区域的面积等于$\frac{3{m}^{2}}{20}$(用m表示);若z=2x-y的最大值与最小值之和为19,则实数m=-10.分析 作出不等式组对应的平面区域,求出交点坐标,利用数形结合即可得到结论.
解答 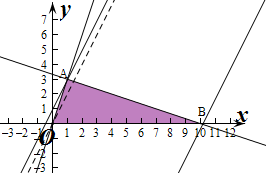 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
当y=0时,x=-m,
由$\left\{\begin{array}{l}{3x-y=0}\\{x+3y+m=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{m}{10}}\\{y=-\frac{3m}{10}}\end{array}\right.$,即A($-\frac{m}{10}$,-$\frac{3m}{10}$),
则三角形OAB的面积S=$\frac{1}{2}×$(-m)(-$\frac{3m}{10}$)=$\frac{3{m}^{2}}{20}$,
由z=2x-y得y=2x-z,
平移直线y=2x-z,由图象可知当直线y=2x-z经过点A($-\frac{m}{10}$,-$\frac{3m}{10}$)时,直线y=2x-z的截距最大,此时z最小.即最小值z=2×($-\frac{m}{10}$)-(-$\frac{3m}{10}$)=$\frac{m}{10}$,
当直线y=2x-z经过点B(-m,0)时,直线y=2x-z的截距最小,此时z最大,
即最大值z=-2m,
∵z=2x-y的最大值与最小值之和为19,
∴-2m+$\frac{m}{10}$=19,
即m=-10.
故答案为:$\frac{3{m}^{2}}{20}$,-10.
点评 本题主要考查线性规划的应用,利用数形结合求出相应的交点坐标是解决本题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
18.设$a=\int_0^π{(sinx-1+2{{cos}^2}\frac{x}{2}})dx$,则多项式${(a\sqrt{x}-\frac{1}{{\sqrt{x}}})^6}•({x^2}+2)$的常数项是( )
| A. | -332 | B. | 332 | C. | 166 | D. | -166 |
18.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2-bc,bc=4,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
1.设等比数列{an}的各项均为正数,若$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{2}$=$\frac{2}{{a}_{1}}$+$\frac{2}{{a}_{2}}$,$\frac{{a}_{3}}{4}$+$\frac{{a}_{4}}{4}$=$\frac{4}{{a}_{3}}$+$\frac{4}{{a}_{4}}$,则a1a5=( )
| A. | 24$\sqrt{2}$ | B. | 8 | C. | 8$\sqrt{2}$ | D. | 16 |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{36}$=1(a>0)的顶点到渐近线的距离为2,则该双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
13.设函数f(x)满足2f′(x)>f(x),则一定成立的是( )
| A. | 3f(2ln2)<2f(2ln3) | B. | 3f(2ln2)>2f(2ln3) | C. | 2f(3ln3)<3f(2ln2) | D. | 2f(3ln3)>3f(2ln2) |
 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点. ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标 的值评定高三学生的幸福感等级:若
的值评定高三学生的幸福感等级:若 ,则幸福感为一级;若
,则幸福感为一级;若 ,则幸福感为二级;若
,则幸福感为二级;若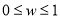 ,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果: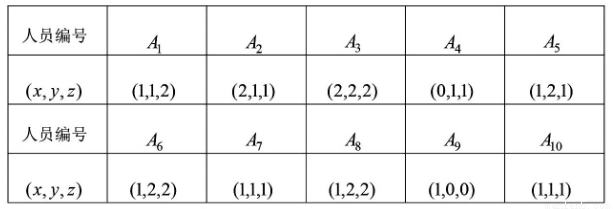
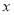 相同的概率;
相同的概率; ,从幸福感等级不是一级的被采访者中任取一人,其综合指标为
,从幸福感等级不是一级的被采访者中任取一人,其综合指标为 ,记随机变量
,记随机变量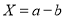 ,求
,求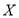 的分布列及其数学期望.
的分布列及其数学期望.