题目内容
在极坐标系下M为曲线ρcos(θ+| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
分析:把曲线的极坐标方程化为普通方程,求出点的直角坐标,利用点到直线的距离公式求出|PM|的最小值.
解答:解:曲线ρcos(θ+
)=
即ρ(
cosθ-
sinθ )=
,∴x-
y-1=0.
∵点P的极坐标为(2
,
),∴点P的直角坐标为(-
,3).
∴|PM|的最小值是点P到x-
y-1=0 的距离:
=
,
故答案为
.
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∵点P的极坐标为(2
| 3 |
| 2π |
| 3 |
| 3 |
∴|PM|的最小值是点P到x-
| 3 |
|-
| ||||
|
4
| ||
| 2 |
故答案为
4
| ||
| 2 |
点评:本题考查把极坐标方程化为普通方程的方法,两角和的余弦公式,点到直线的距离公式的应用.

练习册系列答案
相关题目
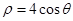 ,过极点的直线
,过极点的直线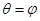 (
( 且
且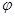 是参数)交曲线C于两点0,A,令OA的中点为M.
是参数)交曲线C于两点0,A,令OA的中点为M. 时,求M点的直角坐标.
时,求M点的直角坐标.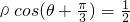 上任意一点,点P的极坐标为
上任意一点,点P的极坐标为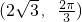 ,则|PM|的最小值是________.
,则|PM|的最小值是________.