题目内容
以坐标原点为极点,横轴的正半轴为极轴的极坐标系下,有曲线C: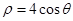 ,过极点的直线
,过极点的直线
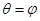 (
( 且
且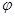 是参数)交曲线C于两点0,A,令OA的中点为M.
是参数)交曲线C于两点0,A,令OA的中点为M.
(1)求点M在此极坐标下的轨迹方程(极坐标形式).
(2)当 时,求M点的直角坐标.
时,求M点的直角坐标.
【答案】
(1)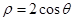 ,(2)
,(2)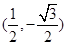
【解析】
试题分析:(1)因为OA的中点为M.,而OA=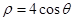 ,所以OM=
,所以OM= OA,点M在此极坐标下的轨迹方程是
OA,点M在此极坐标下的轨迹方程是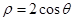 。
。
(2)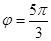 时,
时,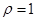 ,所以x=cos
,所以x=cos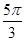 =
= ,y=sin
,y=sin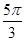 =
=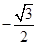 ,即M点的直角坐标是
,即M点的直角坐标是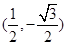 。
。
考点:本题主要考查简单曲线的极坐标方程,直角坐标与极坐标的互化。
点评:简单题,因为OA的中点为M.,所以OM= OA,利用的是几何关系法。
OA,利用的是几何关系法。

练习册系列答案
相关题目
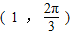 对应的点在以极点为坐标原点,极轴为横轴的直角坐标系的( )
对应的点在以极点为坐标原点,极轴为横轴的直角坐标系的( )