题目内容
1．等差数列{an}的前n项和Sn，若9a5=5a3，则$\frac{{S}_{9}}{{S}_{5}}$=1．分析 由等差数列的求和公式和等差数列的性质可得$\frac{{S}_{9}}{{S}_{5}}$=$\frac{9{a}_{5}}{5{a}_{3}}$，由已知式子可得．
解答 解：∵等差数列{an}的前n项和Sn且9a5=5a3，
∴$\frac{{S}_{9}}{{S}_{5}}$=$\frac{\frac{9（{a}_{1}+{a}_{9}）}{2}}{\frac{5（{a}_{1}+{a}_{5}）}{2}}$=$\frac{9（{a}_{1}+{a}_{9}）}{5（{a}_{1}+{a}_{5}）}$=$\frac{9×2{a}_{5}}{5×2{a}_{3}}$=$\frac{9{a}_{5}}{5{a}_{3}}$=1，
故答案为：1．
点评 本题考查等差数列的求和公式和等差数列的性质，属基础题．
练习册系列答案
相关题目
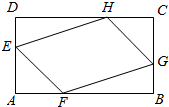如图，在矩形ABCD中，已知AD=1.5，AB=a（a＞1.5），E，F，G，H分别是边AD，AB，BC，CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大，并求最大面积？