题目内容
下列四个命题中,真命题的个数为( )(1)若两平面有三个公共点,则这两个平面重合;(2)两条直线可以确定一个平面;(3)若 ;(4)空间中,相交于同一点的三条直线在同一平面内。
;(4)空间中,相交于同一点的三条直线在同一平面内。
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:(1)若两平面有三个公共点,则这两个平面重合,此命题错误,若两平面相交,两个平面也有三个公共点。
(2)两条直线可以确定一个平面,此命题错误,两条平行或相交直线确定一个平面,但两条异面直线不能确定一个平面。
(3)若 ;此命题正确,若两平面有一个公共点,则两平面有一条过该点的公共直线。
;此命题正确,若两平面有一个公共点,则两平面有一条过该点的公共直线。
(4)空间中,相交于同一点的三条直线在同一平面内。此命题错误,比如空间直角坐标系中在x轴、y轴、z轴。
考点:平面的基本性质与公理。
点评:本题主要考查对公理的理解即把握,熟练掌握平面的基本性质与公理是做本题的关键。

练习册系列答案
相关题目
设 ,
, 是两条不同的直线,
是两条不同的直线,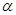 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
如图,在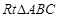 中,
中,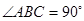 ,
,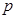 为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为
为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为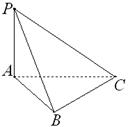
| A.4 | B.3 | C.2 | D.1 |
如果对于空间任意n(n≥2)条直线总存在一个平面α,使得这n条直线与平面α所成的角均相等,那么这样的n( )
| A.最大值为3 | B.最大值为4 | C.最大值为5 | D.不存在最大值 |
设m、n是两条不同的直线,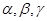 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若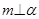 ,
,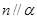 ,则
,则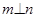 ②若
②若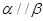 ,
,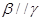 ,
,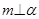 ,则
,则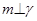
③若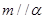 ,
,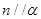 ,则
,则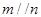 ④若
④若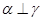 ,
, 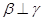 ,则
,则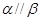
其中正确命题的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①②③④ |
已知直线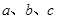 及平面
及平面 ,它们具备下列哪组条件时,有
,它们具备下列哪组条件时,有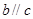 成立( )
成立( )
A.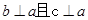 | B. |
C.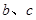 和 和 所成的角相等 所成的角相等 | D.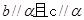 |
在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是( )
| A.4条 | B.6条 | C.8条 | D.10条 |
二面角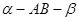 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面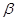 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
已知空间三条直线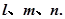 若
若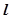 与
与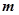 异面,且
异面,且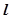 与
与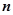 异面,则( )
异面,则( )
A.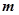 与 与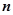 异面. 异面. | B.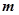 与 与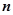 相交. 相交. |
C.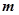 与 与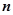 平行. 平行. | D.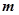 与 与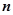 异面、相交、平行均有可能. 异面、相交、平行均有可能. |