题目内容
命题P:方程
+
=1表示双曲线,命题q:不等式x2-2x+k2-1>0对一切实数x恒成立.
(1)求命题P中双曲线的焦点坐标;
(2)若命题“p且q”为真命题,求实数k的取值范围.
| x2 |
| k-2 |
| y2 |
| k-1 |
(1)求命题P中双曲线的焦点坐标;
(2)若命题“p且q”为真命题,求实数k的取值范围.
(1)因为k-1>k-2,所以a2=k-1,b2=k-2…(2分)
所以c2=1,且焦点在y轴上,…(4分)
所以双曲线的焦点坐标为(0,±1).…(6分)
(2)命题p:(k-2)(k-1)<0,1<k<2;…(8分)
命题q:△=4-4(k2-1)<0,k<-
或k>
.…(10分)
因为命题“p且q”为真命题,所以
即
<k<2.…(14分)
(注:若第(1)问分类讨论答案对也算对)
所以c2=1,且焦点在y轴上,…(4分)
所以双曲线的焦点坐标为(0,±1).…(6分)
(2)命题p:(k-2)(k-1)<0,1<k<2;…(8分)
命题q:△=4-4(k2-1)<0,k<-
| 2 |
| 2 |
因为命题“p且q”为真命题,所以
|
| 2 |
(注:若第(1)问分类讨论答案对也算对)

练习册系列答案
相关题目
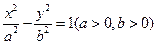 的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段
的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段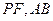 为直径的两圆的位置关系为
为直径的两圆的位置关系为