题目内容
在△ABC中,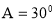 ,
,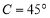 ,
,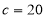 ,则边
,则边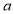 的长为( )
的长为( )
A.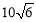 B.
B.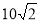 C.
C.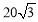 D.
D.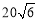
B
【解析】
试题分析:解三角形问题,一般用正余弦定理解决.本题已知两角及一对边,用正弦定理: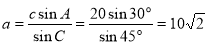
考点:正余弦定理

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
题目内容
在△ABC中,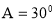 ,
,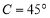 ,
,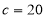 ,则边
,则边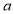 的长为( )
的长为( )
A.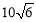 B.
B.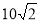 C.
C.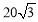 D.
D.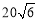
B
【解析】
试题分析:解三角形问题,一般用正余弦定理解决.本题已知两角及一对边,用正弦定理: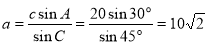
考点:正余弦定理

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案