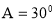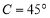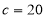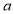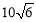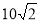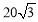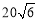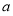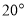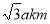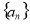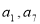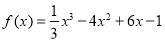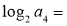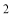Question

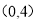设椭圆过点，离心率为.

（1）求椭圆的方程；

（2）求过点且斜率为的直线被椭圆所截得线段的中点坐标.

 

Answer 1

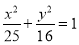（1）；（2）.

【解析】

试题分析：(1)由椭圆过已知点和椭圆的离心率可以列出方程组，解方程组即可，也可以分步求解；(2)直线方程和椭圆方程组成方程组，可以求解，也可以利用根与系数的关系；然后利用中点坐标公式求解即可.

试题解析：（1）将点代入椭圆C的方程得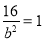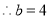， 1分

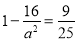由，得， 3分

椭圆C的方程为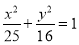 4分

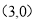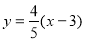（2）过点且斜率为的直线为 5分

设直线与椭圆C的交点为，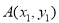

将直线方程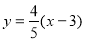代入椭圆C方程，整理得 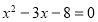7分

由韦达定理得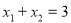

10分

由中点坐标公式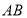中点横坐标为，纵坐标为

所以所截线段的中点坐标为 12分.

考点：1.椭圆的标准方程及其几何性质；2.直线的方程；3.直线与椭圆的位置关系问题.