题目内容
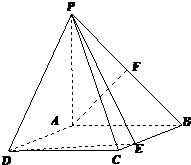如图，四棱锥P-ABCD的底面为矩形，PA是四棱锥的高，PB与DC所成角为45°，F是PB的中点，E是BC上的动点．（Ⅰ）证明：PE⊥AF；
（Ⅱ）若BC=2BE=2
| 3 |
分析：（Ⅰ）建立空间直角坐标系，求出各点的坐标，以及向量PE，AF的坐标，得到其数量积为0即可证明结论．
（Ⅱ）先根据条件求出D的坐标以及
，
的坐标，进而求出平面PDE的法向量的坐标，再代入向量的夹角计算公式即可得到答案．
（Ⅱ）先根据条件求出D的坐标以及
| PD |
| PE |
解答：解：（Ⅰ） 建立如图所示空间直角坐标系．设AP=AB=2，BE=a
则A（0，0，0），B（0，2，0），P（0，0，2），F（0，1，1），E（a，2，0）
于是，
=(a，2，-2)，
=(0，1，1)，
则
•
=0，
所以AF⊥PE．…（6分）
（Ⅱ）若BC=2BE=2
AB，则D(4
，0，0)，
=(4
，0，-2)，
=（2
，2，-2），
设平面PDE的法向量为
=（x，y，z），
由
，得：
，令x=1，则z=2
，y=
，
于是
=(1，
，2
)，而
=(0，0，2)
设直线AP与平面PDE所成角为θ，
则sinθ=
=
．
∴直线AP与平面PDE所成角为60°．
则A（0，0，0），B（0，2，0），P（0，0，2），F（0，1，1），E（a，2，0）
于是，
| PE |
| AF |
则
| PE |
| AF |
所以AF⊥PE．…（6分）
（Ⅱ）若BC=2BE=2
| 3 |
| 3 |
| PD |
| 3 |
| PE |
| 3 |
设平面PDE的法向量为
| n |
由
|
|
| 3 |
| 3 |
于是
| n |
| 3 |
| 3 |
| AP |
设直线AP与平面PDE所成角为θ，
则sinθ=
|
| ||||
|
|
| ||
| 2 |
∴直线AP与平面PDE所成角为60°．
点评：本题主要考察用空间向量求直线与平面的夹角以及用向量语言表述线线的垂直．在利用向量语言表述线线的垂直关系时，只要得到数量积为0即可．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=