题目内容

已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2-2x
（1）求函数f（x）的解析式，并画出函数f（x）的图象．
（2）根据图象写出的单调区间和值域．
（1）由x≥0时，f（x）=x2-2x，
当x＜0时，-x＞0，
∴f（-x）=x2+2x
又函数f（x）为偶函数，
∴f（x）=x2+2x-------------3’
故函数的解析式为f(x)=
x2-2x(x≥0)
x2+2x(x＜0)
-------------4’
函数图象如下图所示：--------------7’

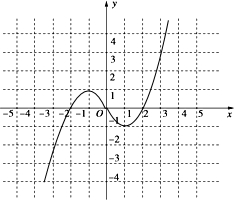
（2）由函数的图象可知，
函数f（x）的单调递增区间为[-1，0]、[1，+∞）
单调递减区间为（-∞，-1]、[0，1]，
函数f（x）的值域为[-1，+∞）------12’
练习册系列答案
相关题目
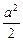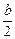已知f(x)、g(x)都是奇函数，f(x)＞0的解集是(a2，b)，g(x)＞0的解集是(，)，
则f(x)·g(x)＞0的解集是__________．
已知函数f(x)=
ax+b
x2+1
在点M(1，f(1))处的切线方程为x-y-1=0．
（Ⅰ）求f（x）的解析式；
（Ⅱ）设函数g（x）=lnx，证明：g（x）≥f（x）对x∈[1，+∞）恒成立．
下列函数中既不是奇函数，又不是偶函数的是（　　）
A．y=2|x|B．y=lg(x+
x2+1
)		C．y=2x+2-xD．y=lg
1
x+1
已知函数f（x）=a-
2
2x+1

（1）若f（x）为奇函数，求实数a的值；
（2）判断并证明f（x）的单调性．
已知命题p：1-a•2x≥0在x∈（-∞，0]恒成立，命题q：?x∈R，ax2-x+a＞0．若命题p或q为真，命题p且q为假，求实数a的范围．
已知函数f(x)=1-
2
3x+1
．
（1）求函数f（x）的定义域并判断函数f（x）的奇偶性；
（2）用单调性定义证明：函数f（x）在其定义域上都是增函数；
（3）解不等式：f（3m2-m+1）+f（2m-3）＜0．
设函数f（x）=x2-1，对任意x∈[
3
2
，+∞），f（
x
m
）-4m2f（x）≤f（x-1）+4f（m）恒成立，则实数m的取值范围是______．
已知函数f（x）是定义在R上的偶函数，且f（x）在区间（-∞，0）上是减函数，若f（x-1）＜f（2），则实数x的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网