题目内容
17.数列{an}中,a1=sinθ,an+1=an•cosθ(n∈N*,sinθ,cosθ≠0),若$\underset{lim}{n→∞}$(a1+a2+…+an)=$\sqrt{3}$,求θ分析 由sinθ,cosθ≠0,可得数列{an}是以sinθ为首项,以cosθ为公比的等比数列,由数列的极限等于$\sqrt{3}$列式,再由辅助角公式化积后求得θ.
解答 解:∵sinθ,cosθ≠0,∴数列{an}是以sinθ为首项,以cosθ为公比的等比数列,
则$\underset{lim}{n→∞}$(a1+a2+…+an)=$\frac{sinθ}{1-cosθ}$=$\sqrt{3}$,
即sinθ+$\sqrt{3}cosθ=\sqrt{3}$.
∴2($\frac{1}{2}$sinθ+$\frac{\sqrt{3}}{2}$cosθ)=$\sqrt{3}$,即sin(θ+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$.
∴θ+$\frac{π}{3}$=$\frac{π}{3}+2kπ$或$θ+\frac{π}{3}=\frac{2π}{3}+2kπ,k∈Z$.
则θ=2kπ(舍)或$θ=\frac{π}{3}+2kπ,k∈Z$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了数列极限的求法,是中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.已知等差数列{an}的前n项和为Sn,且满足a1=9,S5=35,则使Sn取最大值的n的值为( )
| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
12.填表:
| 角α | 0° | 90° | 180° | 270° | 360° |
| α的弧度数 | |||||
| sinα | |||||
| cosα | |||||
| tanα |
5.设等差数列{an}的公差为d,则a1d>0是数列{${3}^{{a}_{1}{a}_{n}}$}为递增数列的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
 中,
中,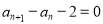 ,且
,且 ,则
,则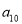 等于( )
等于( )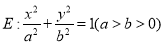 的右焦点为
的右焦点为 .短轴的一个端点为
.短轴的一个端点为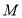 ,直线
,直线 交椭圆
交椭圆 于
于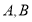 两点.若
两点.若 ,点
,点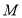 到直线
到直线 的距离不小于
的距离不小于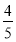 ,则椭圆
,则椭圆 B.
B.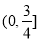 C.
C.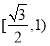 D.
D.