题目内容
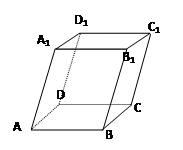
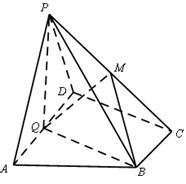
(本小题满分12分)已知四棱锥 中
中 平面
平面 ,
,
且 ,底面为直角梯形,
,底面为直角梯形,
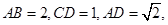
 分别是
分别是 的中点.
的中点.

(1)求证: // 平面
// 平面 ;
;
(2)求截面 与底面
与底面 所成二面角的大小;
所成二面角的大小;
(3)求点 到平面
到平面 的距离.
的距离.
 中
中 平面
平面 ,
,且
 ,底面为直角梯形,
,底面为直角梯形,
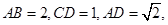
 分别是
分别是 的中点.
的中点.
(1)求证:
 // 平面
// 平面 ;
;(2)求截面
 与底面
与底面 所成二面角的大小;
所成二面角的大小;(3)求点
 到平面
到平面 的距离.
的距离.(1)只需证 //平面
//平面 ;(2)
;(2) ;(3)
;(3)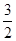 。
。
 //平面
//平面 ;(2)
;(2) ;(3)
;(3)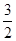 。
。试题分析:以
 为原点,以
为原点,以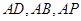 分别为
分别为 建立空间直角坐标系
建立空间直角坐标系 ,
,由
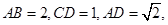
 ,
, 分别是
分别是 的中点,
的中点,可得:
 ,
,
∴
 ,
, ………2分
………2分 设平面的
 的法向量为
的法向量为 ,
,则有:

令
 ,则
,则 , ……………3分
, ……………3分∴
 ,又
,又 平面
平面
∴
 //平面
//平面 ……………4分
……………4分(2)设平面的
 的法向量为
的法向量为 ,又
,又
则有:

令
 ,则
,则 , …………6分
, …………6分又
 为平面
为平面 的法向量,∴
的法向量,∴ ,又截面
,又截面 与底面
与底面 所成二面角为锐二面角,
所成二面角为锐二面角,∴截面
 与底面
与底面 所成二面角的大小为
所成二面角的大小为 …………8分
…………8分(3)∵
 ,
,∴所求的距离
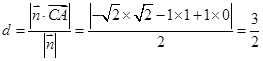 …12分
…12分点评:综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面
 的两个半平面内与棱
的两个半平面内与棱 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量 与
与 的夹角; ②设
的夹角; ②设 分别是二面角
分别是二面角 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 AD=1,CD=
AD=1,CD=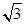 .
.
 α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m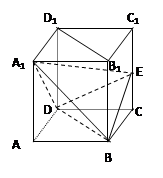
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F.
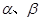 表示两个互相垂直的平面,
表示两个互相垂直的平面,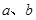 表示一对异面直线,则
表示一对异面直线,则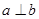 的一个充分条件是( )
的一个充分条件是( )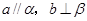 B.
B.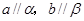
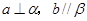 D.
D.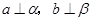
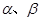 和两条不重合的直线
和两条不重合的直线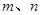 ,有下列四个命题:
,有下列四个命题: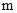 //
//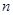 ,
,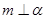 ,则
,则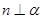 ; ②若
; ②若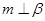 ,则
,则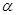 //
//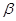 ;
;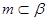 ,则
,则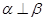 ; ④若
; ④若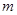 //
//