题目内容
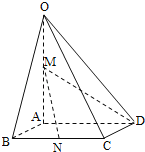
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为 2 的正三角形,顶点
是边长为 2 的正三角形,顶点 ![]() 在底面
在底面![]() 上的射影为
上的射影为![]() 的中心,若
的中心,若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵定点A在底面BCD上的射影为三角形BCD的中心,
而且底面BCD是正三角形,
∴三棱锥A﹣BCD是正三棱锥,∴AB=AC=AD,
令底面三角形BCD的重心(即中心)为P,
∵底面BCD为边长为2的正三角形,DE是BC边上的高,
∴DE=![]() ,∴PE=
,∴PE=![]() ,DP=
,DP=![]()
∵直线AE与底面BCD所成角的正切值为2![]() ,即
,即![]()
∴AP=![]() ,
,
∵AD2=AP2+DP2(勾股定理),∴AD=2,于是AB=AC=AD=BC=CD=DB=2,
∴三棱锥为正四面体,构造正方体,由面上的对角线构成正四面体,故正方体的棱长为![]() ,
,
∴正方体的对角线长为![]() ,∴外接球的半径为
,∴外接球的半径为![]() .
.
∴外接球的表面积=4πr2=6π.
故选D.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目