题目内容
平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足 =α
=α +β
+β ,其中α,β∈R且α+β=1,则点C的轨迹方程为( )
,其中α,β∈R且α+β=1,则点C的轨迹方程为( )
| A.(x-1)2+(y-2)2=5 | B.3x+2y-11=0 |
| C.2x-y=0 | D.x+2y-5=0 |
D
解析

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
△ABC的外接圆的圆心为O,半径为2,且 ,则向量
,则向量 在
在 方向上的投影为( )
方向上的投影为( )
A. | B.3 | C. | D.-3 |
若 ·
· +
+ <0,则△ABC必定是( )
<0,则△ABC必定是( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.等腰直角三角形 |
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
| A.θ=π | B.θ= |
C.θ= | D.θ= |
圆C:x2+y2=1,直线l:y=kx+2,直线l与圆C交于A,B,若| +
+ |<|
|<| -
- |(其中O为坐标原点),则k的取值范围是( )
|(其中O为坐标原点),则k的取值范围是( )
A.(0, ) ) | B.(- , , ) ) |
C.( ,+∞) ,+∞) | D.(-∞,- )∪( )∪( ,+∞) ,+∞) |
已知O是△ABC所在平面内一点,D为BC边中点,且2 +
+ +
+ =0,那么( )
=0,那么( )
A. = = | B. =2 =2 |
C. =3 =3 | D.2 = = |
椭圆 =1上有两个动点P,Q,E(3,0),EP⊥EQ,则
=1上有两个动点P,Q,E(3,0),EP⊥EQ,则 ·
· 的最小值为( ).
的最小值为( ).
| A.6 | B.3- | C.9 | D.12-6 |
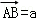 ,
, ,则
,则 =( )
=( )
 B.
B. C.
C. D.
D.



