Question

【题目】如图，在中，已知点D在边AB上，AD=3DB，

， ，BC=13.

（1）求的值；

（2）求CD的长.

Answer 1

【答案】(1) (2)9

【解析】试题分析：（1）在△ABC中，求出sinA=，sin∠ACB=,

可得cosB=-cos（A+∠ACB）=sinAsin∠ACB-cosAcosB；
（2）在△ABC中，由正弦定理得，AB= ∠ACB.
在△BCD中，由余弦定理得，CD=代入即得解.

试题解析：

(1)在△ABC中, cosA=,A，

所以 sinA=.

同理可得sin∠ACB=.

所以cosB=-cos（ –(A+∠ACB）)= -cos（A+∠ACB）=sinAsin∠ACB-cosAcosB=.

(2)在△ABC中,由正弦定理得, AB= ∠ACB =.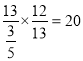

又AD=3DB,所以

又在△BCD 中,由余弦定理得,

CD=