题目内容
设函数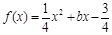 ,已知
,已知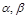 不论为何实数时,恒有
不论为何实数时,恒有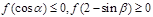 ,对于正数数列
,对于正数数列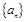 ,其前项和
,其前项和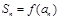 (
(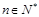 )
)
(1)求 的值;
的值;
(2)求数列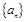 的通项公式;
的通项公式;
(3)是否存在等比数列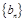 ,使得
,使得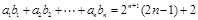 对一切正整数
对一切正整数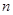 都成立,并证明你的结论;
都成立,并证明你的结论;
(4)若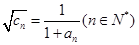 ,且数列
,且数列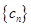 的前
的前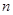 项和为
项和为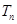 ,比较
,比较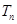 与
与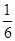 的大小。
的大小。
【答案】
解:(1)令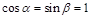 ,则
,则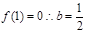
(2)由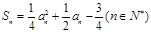 可得
可得
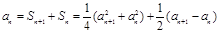
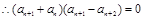
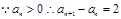
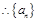 是等差数列
是等差数列 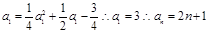
(3)假设存在等比数列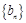 ,使得
,使得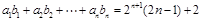 对一切正整数
对一切正整数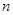 都成立.
都成立.
当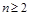 时,
时,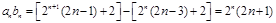
又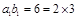 故
故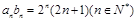
令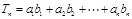
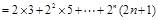
则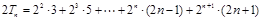
两式相减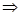
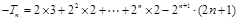

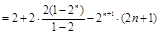
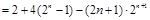
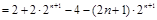
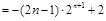 .
.
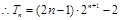 成立
成立
(4)由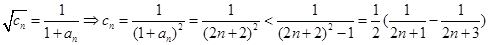
所以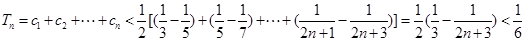
所以
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
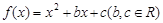 ,已知不论
,已知不论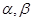 为何实数恒有
为何实数恒有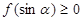 ,
,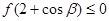
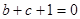 ;
;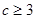 ;
;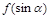 的最大值为8,求
的最大值为8,求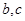 值.
值. ,已知不论
,已知不论 为何实数,恒有
为何实数,恒有 和
和 。
。
 的最大值为8,求b、c的值。
的最大值为8,求b、c的值。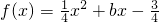 ,已知不论α、β为何实数,恒有f(cosα)≤0,f(2-sinβ)≥0,求b=________.
,已知不论α、β为何实数,恒有f(cosα)≤0,f(2-sinβ)≥0,求b=________.