题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:当 当 所以 |
(2) |
解:因为 所以 两式相减,得: 因为 |
(3) |
解:探索:以 令 所以 ①-②:
所以 即存在等比数列 |

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ;
;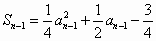 ,
,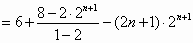
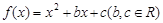 ,已知不论
,已知不论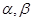 为何实数恒有
为何实数恒有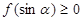 ,
,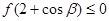
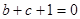 ;
;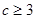 ;
;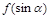 的最大值为8,求
的最大值为8,求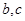 值.
值. ,已知不论
,已知不论 为何实数,恒有
为何实数,恒有 和
和 。
。
 的最大值为8,求b、c的值。
的最大值为8,求b、c的值。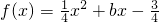 ,已知不论α、β为何实数,恒有f(cosα)≤0,f(2-sinβ)≥0,求b=________.
,已知不论α、β为何实数,恒有f(cosα)≤0,f(2-sinβ)≥0,求b=________.