题目内容
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
C
解析试题分析:∵函数f (x)=x3-4x+a,0<a<2,∴f′(x)=3x2-4.令f′(x)=0,得 x=±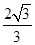 .∵当x<-
.∵当x<-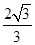 时,f′(x)>0;在(-
时,f′(x)>0;在(-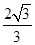 ,
,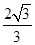 )上,f′(x)<0;在(
)上,f′(x)<0;在(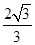 ,+∞)上,f′(x)>0.故函数在(-∞,-
,+∞)上,f′(x)>0.故函数在(-∞,-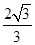 )上是增函数,在(-
)上是增函数,在(-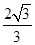 ,
,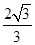 )上是减函数,在(
)上是减函数,在(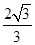 ,+∞)上是增函数.故f(-
,+∞)上是增函数.故f(-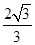 )是极大值,f(
)是极大值,f(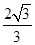 )是极小值.再由f (x)的三个零点为x1,x2,x3,且x1<x2<x3,得 x1<-
)是极小值.再由f (x)的三个零点为x1,x2,x3,且x1<x2<x3,得 x1<-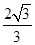 ,-
,-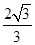 <x2<
<x2<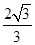 ,x3>
,x3>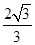 .根据f(0)=a>0,且f(
.根据f(0)=a>0,且f(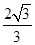 )=a-
)=a-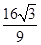 <0,得
<0,得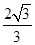 >x2>0.∴0<x2<1.故选C.
>x2>0.∴0<x2<1.故选C.
考点:本题考查了导函数的运用
点评:本题函数的零点的定义,函数的零点与方程的根的关系,利用导数研究函数的单调性,利用导数求函数的极值,属于中档题.

练习册系列答案
相关题目
由曲线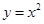 与
与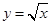 的边界所围成区域的面积为
的边界所围成区域的面积为
A.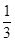 | B.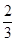 | C.1 | D.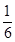 |
若函数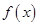 在R 上可导,且满足
在R 上可导,且满足 ,则( )
,则( )
A.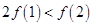 | B.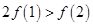 | C.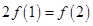 | D.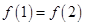 |
设曲线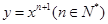 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为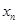 ,则
,则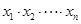 的值为
的值为
A.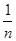 | B.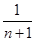 | C.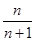 | D.1 |
函数 =
=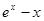 (
(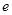
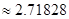 )在区间[-1,1]上的最大值是( )
)在区间[-1,1]上的最大值是( )
A.1+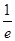 | B.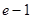 | C.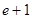 | D.1 |
一个物体的运动方程为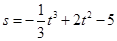 ,其中
,其中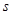 的单位是米,
的单位是米,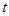 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
根据定积分的几何意义,计算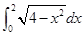 的结果是( )
的结果是( )
A.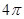 | B.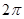 | C.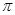 | D.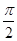 |
设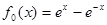 ,且对任意的
,且对任意的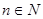 ,都有
,都有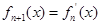 ,则
,则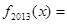
A.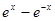 | B.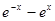 | C.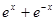 | D.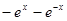 |
已知函数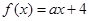 ,若
,若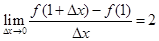 ,则实数
,则实数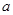 的值为( )
的值为( )
A.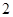 | B.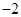 | C.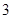 | D.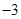 |