题目内容
【题目】如图1,在矩形ABCD中,AB=8,AD=3,点E,F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G、H分别在A1B、D1C上,A1G=D1H= ![]() ,过点G、H的平面α与几何体A1EB﹣D1FC的面相交,交线围成一个正方形.
,过点G、H的平面α与几何体A1EB﹣D1FC的面相交,交线围成一个正方形. 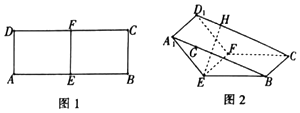
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求点E到平面α的距离.
【答案】
(1)解:如图所示:

(2)解:过E作EP⊥GM,垂足为P,连接HP,
∵EF⊥A1E,EF⊥BE,A1E∩BE=E,
∴EF⊥平面A1BE,
∵A1G=D1H,∴GH∥EF,
∴GH⊥平面A1BE,又EP平面A1BE,
∴EP⊥GH,又GH∩GM=G,GH平面GHNM,GM平面GHNM,
∴EP⊥平面GHNM,
由(1)可知GM∥A1E,EM=1,
∴∠PEM=30°,
∴PM= ![]() ,PE=
,PE= ![]() =
= ![]() ,
,
∴点E到平面α的距离为 ![]() .
.
【解析】解:(1)由题意可知A1E=BE=4,GH=A1D1=3, 在△A1BE中,由余弦定理得A1B= ![]() =4
=4 ![]() ,
,
设平面α与几何体的截面正方形为GHNM,则GM=3,
若M在棱BE上,设BM=x,则由余弦定理得cos30°= ![]() =
= ![]() ,解得x=3,
,解得x=3,
若M在棱A1E上,设A1M=x,
则由余弦定理得cos30°= ![]() =
= ![]() ,解得x=9(舍).
,解得x=9(舍).
过M作MN∥EF交CF于N,连接GH,MN,GM,HN,
则正方形GHNM即为要作的正方形.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

