题目内容
【题目】已知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 ![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设点为P(x,y)为直线l与圆C所截得的弦上的动点,求 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)因为圆C的极坐标方程为 ![]() , 所以
, 所以 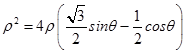 ,
,
所以圆C的普通方程 ![]() .
.
(Ⅱ)由圆C的方程 ![]() ,可得
,可得 ![]() ,
,
所以圆C的圆心是 ![]() ,半径是2,
,半径是2,
将 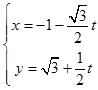 代入
代入 ![]() 得
得 ![]() ,
,
又直线l过 ![]() ,圆C的半径是2,所以﹣2≤t≤2,
,圆C的半径是2,所以﹣2≤t≤2,
即 ![]() 的取值范围是[﹣2,2]
的取值范围是[﹣2,2]
【解析】(Ⅰ)把圆C的极坐标方程转化为 ![]() ,由此能求出圆C的普通方程.(Ⅱ)求出圆C的圆心是
,由此能求出圆C的普通方程.(Ⅱ)求出圆C的圆心是 ![]() ,半径是2,将
,半径是2,将 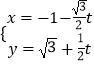 代入
代入 ![]() 得
得 ![]() ,由此能求出
,由此能求出 ![]() 的取值范围.
的取值范围.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目