题目内容
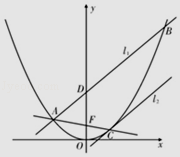
【题目】已知抛物线的方程为C:x2=4y,过点Q(0,2)的一条直线与抛物线C交于A,B两点,若抛物线在A,B两点的切线交于点P.
(1)求点P的轨迹方程;
(2)设直线PQ与直线AB的夹角为α,求α的取值范围.
【答案】
(1)
解:由AB直线与抛物线交于两点可知,直线AB不与x轴垂直,故可设lAB:y=kx+2,
则 ![]() ,整理得:x2﹣4ky﹣8=0…①,
,整理得:x2﹣4ky﹣8=0…①,
△=16k2+32>0,故k∈R时均满足题目要求.
设交点坐标为 ![]() ,则x1,x2为方程①的两根,
,则x1,x2为方程①的两根,
故由韦达定理可知,x1+x2=4k,x1x2=﹣8.
将抛物线方程转化为 ![]() ,则
,则 ![]() ,故A点处的切线方程为
,故A点处的切线方程为 ![]() ,
,
整理得 ![]() ,
,
同理可得,B点处的切线方程为 ![]() ,记两条切线的交点P(xp,yp),
,记两条切线的交点P(xp,yp),
联立两条切线的方程,解得点P坐标为 ![]() ,
,
故点P的轨迹方程为y=﹣2,x∈R
(2)
解:当k=0时,xP=0,yP=﹣2,此时直线PQ即为y轴,与直线AB的夹角为 ![]() .
.
当k≠0时,记直线PQ的斜率 ![]() ,
,
又由于直线AB的斜率为k,且已知直线AB与直线PQ所夹角α∈[0, ![]() ],
],
tanα=丨 ![]() 丨=丨
丨=丨 ![]() 丨=
丨= ![]() +丨k丨≥2
+丨k丨≥2 ![]() ,
,
则a∈[arctan2 ![]() ,
, ![]() )
)
综上所述,α的取值范围是∈[arctan2 ![]() ,
, ![]() ]
]
【解析】(1)将直线AB的方程代入椭圆方程,利用韦达定理及导数的几何意义,分别求得切线方程,联立即可求得点P的轨迹方程;(2)分类讨论,根据直线斜率与倾斜角的关系,即可求得tanα取值范围,即可求得α的取值范围.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量(个) | 频数 | 频率 |
0~4 | 0.15 | |
5~8 | 40 | 0.4 |
9~12 | 25 | |
13~16 | a | c |
16以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值及样本中微信群个数超过12的概率;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).