题目内容
1.若直线y=kx与曲线y=x2+x所围成的封闭图形的面积为$\frac{1}{12}$,则k=1+$\frac{\root{3}{4}}{2}$或1-$\frac{\root{3}{4}}{2}$.分析 先根据题意画出区域,然后依据图形得到积分下限和积分上限,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义建立等式,即可求出k的值
解答 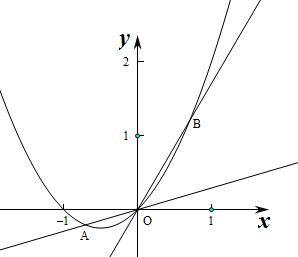 解:函数的导数为f′(x)=2x+1,则f′(0)=1,
解:函数的导数为f′(x)=2x+1,则f′(0)=1,
将y=kx代入y=x2+x得x=0或x=k-1,
若k>1,则对应的面积S=${∫}_{0}^{k-1}$(kx-x2-x)dx=[$\frac{1}{2}$(k-1)x2-$\frac{1}{3}x$3]|${\;}_{0}^{k-1}$
=[$\frac{1}{2}$(k-1)3-$\frac{1}{3}$(k-1)3]=$\frac{1}{6}$(k-1)3=$\frac{1}{12}$,
即(k-1)3=$\frac{1}{2}$,即k-1=$\root{3}{\frac{1}{2}}$=$\frac{\root{3}{4}}{4}$,即k=$\frac{\root{3}{4}}{4}$+1,
若k<1,则对应的面积S=${∫}_{k-1}^{0}$(kx-x2-x)dx=[$\frac{1}{2}$(k-1)x2-$\frac{1}{3}x$3]|${\;}_{k-1}^{0}$
=-[$\frac{1}{2}$(k-1)3-$\frac{1}{3}$(k-1)3]=-$\frac{1}{6}$(k-1)3=$\frac{1}{12}$,
即(k-1)3=-$\frac{1}{2}$,即k-1=-$\root{3}{\frac{1}{2}}$=-$\frac{\root{3}{4}}{2}$,即k=1-$\frac{\root{3}{4}}{2}$,
综上k=1+$\frac{\root{3}{4}}{2}$或k=1-$\frac{\root{3}{4}}{2}$,
故答案为:1+$\frac{\root{3}{4}}{2}$或1-$\frac{\root{3}{4}}{2}$.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于中档题

| A. | a-b=0的充要条件是$\frac{a}{b}$=1 | B. | ?x∈R,ex>xe | ||
| C. | ?x0∈R,|x0|≤0 | D. | 若p∧q为假,则p∨q为假 |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |