题目内容
已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率
,离心率![]() ,右准线方程为
,右准线方程为![]() 。w.w.w.k.s.5.u.c.o.m
。w.w.w.k.s.5.u.c.o.m ![]()
![]()
(I)求椭圆的标准方程;
(II)过点解析:(Ⅰ)由条件有 ,解得
,解得![]() 。
。
![]()
![]() 。
。
所以,所求椭圆的方程为![]()
![]() 。…………………………………4分
。…………………………………4分
(Ⅱ)由(Ⅰ)知![]() 、
、![]() 。
。
若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为x=-1,中点的横坐标就是-1,
的方程为x=-1,中点的横坐标就是-1,
与题设矛盾。
![]() 直线
直线![]() 的斜率存在。
的斜率存在。
设直线l的斜率为k,则直线的方程为y=k(x+1)。
设![]() 、
、![]() ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m ![]()
![]()
联立 ,消y得
,消y得![]() 。
。
由根与系数的关系知![]() ,
,
![]() ,
,
解得![]() ,
,
![]()

练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点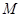 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.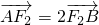 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆