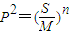题目内容
若等比数列的各项均为正数,前n项之和为S,前n项之积为P,前n项倒数之和为M,则
- A.
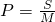
- B.
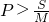
- C.
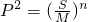
- D.
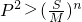
C
分析:先设此等比数列的首项为a1,公比为q.分当q=1和q≠1时,用a1,q分别表示出S,P和M,进而得出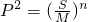
解答:设此等比数列的首项为a1,公比为q
若q=1,则S=na1,M= ,P=a1n,所以P2=a12n,
,P=a1n,所以P2=a12n, =a12n所以
=a12n所以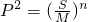 .
.
若q≠1,则S= ,M=
,M= =
= ,P=a1nq
,P=a1nq
所以 =[a12qn-1]n=a12nq[n(n-1)]
=[a12qn-1]n=a12nq[n(n-1)]
P2=a12nq[n(n-1)]
所以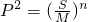
故选C.
点评:题考查等比数列的通项公式、前n项和.及计算能力.在用a1,q表示S 是要分 当q=1和q≠1两种情况.
分析:先设此等比数列的首项为a1,公比为q.分当q=1和q≠1时,用a1,q分别表示出S,P和M,进而得出
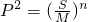
解答:设此等比数列的首项为a1,公比为q
若q=1,则S=na1,M=
 ,P=a1n,所以P2=a12n,
,P=a1n,所以P2=a12n, =a12n所以
=a12n所以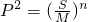 .
.若q≠1,则S=
 ,M=
,M= =
= ,P=a1nq
,P=a1nq
所以
 =[a12qn-1]n=a12nq[n(n-1)]
=[a12qn-1]n=a12nq[n(n-1)]P2=a12nq[n(n-1)]
所以
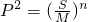
故选C.
点评:题考查等比数列的通项公式、前n项和.及计算能力.在用a1,q表示S 是要分 当q=1和q≠1两种情况.

练习册系列答案
相关题目