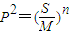Question

若等比数列的各项均为正数，前n项之和为S，前n项之积为P，前n项倒数之和为M，则下列关系成立的是

③

．                                                              　　　　　　　                  
①P=

S

M

；②P＞

S

M

；③P2=(

S

M

)n；④P²＞(

S

M

)n．

Answer 1

分析：设出等比数列的首项和公比，分公比等于1和不等于1分类求出前n项之和为S，前n项之积为P，前n项倒数之和为M，验证后可知③成立．

解答：解：设此等比数列的首项为a₁，公比为q
若q=1，则S=na₁，M=

n

a1

，P=a1n，∴P2=a12n，(

S

M

)n=a12n，
若q不等于1，则S=

a1(qn-1)

q-1

，M=

1-( 1 q )n

a1(1- 1 q )

=

qn-1

a1(qn-qn-1)

，P=a1n•q

n(n-1)

2

所以(

S

M

)n=(a12•qn-1)n=a12n•qn(n-1)
P2=a12n•qn(n-1)．
∴P2=(

S

M

)n．
故答案为③．

点评：本题考查了等比数列的性质，考查了分类讨论的数学思想方法，考查了学生的计算能力，是中档题．