题目内容
设函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为
(1)确定 的值
的值
(2)若过点(0,2)可做曲线 的三条不同切线,求
的三条不同切线,求 的取值范围
的取值范围
(3)设曲线 在点
在点 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当 时,
时,
【答案】
(1)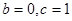
(2)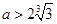
(3)运用反证法来加以证明即可。
【解析】
试题分析:(1)根据题意,由于函数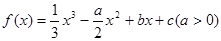 ,曲线
,曲线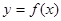 在点
在点 处的切线方程为
处的切线方程为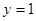
则可知f’(0)=0,得到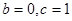 ,
,
(2)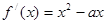 ,设曲线上的任意一点为
,设曲线上的任意一点为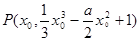 ,则在点P处的切线的方程为
,则在点P处的切线的方程为
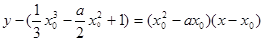 ,又直线过点
,又直线过点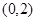
所以,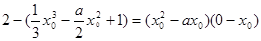 ,化简得
,化简得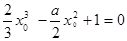
设 ,易知
,易知

(3)反证法:由题知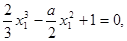
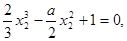
两式作差得
若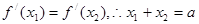 ,将其带入
,将其带入
得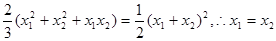 ,
,
与已知矛盾
考点:导数的运用
点评:主要是考查了导数的几何意义以及函数的最值问题,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,曲线
,曲线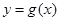 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的斜率为
处切线的斜率为 C.
C. D.
D.
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点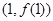 处切线的斜率为( )
处切线的斜率为( )  B.2 C.4
D.
B.2 C.4
D.
 ,曲线
,曲线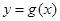 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点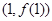 处切线的斜率为( )
处切线的斜率为( ) B.
B. C.
C. D.
D.
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线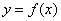 在点
在点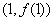 处的切线方程为 (
)
处的切线方程为 (
) B.
B. C.
C. D.
D.