题目内容
(海南宁夏卷文21)设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
【试题解析】1)方程![]() 可化为
可化为![]() ,当
,当![]() 时,
时,![]() ;
;
又![]() ,于是
,于是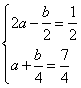 ,解得
,解得![]() ,故
,故![]()
(2)设![]() 为曲线上任一点,由
为曲线上任一点,由![]() 知曲线在点
知曲线在点![]() 处的切线方程为
处的切线方程为
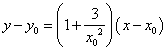 ,即
,即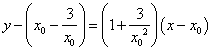
令![]() ,得
,得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为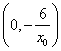 ;
;
令![]() ,得
,得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为![]() ;
;
所以点![]() 处的切线与直线
处的切线与直线![]() 所围成的三角形面积为
所围成的三角形面积为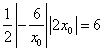 ;
;
故曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 所围成的三角形面积为定值,此定值为6;
所围成的三角形面积为定值,此定值为6;

练习册系列答案
相关题目