题目内容
在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对一切实数x都成立.求实数a的取值范围.分析:根据新定义化简不等式,得到a2-a-1<x2-x因为不等式恒成立,即要a2-a-1小于x2-x的最小值,先求出x2-x的最小值,列出关于a的一元二次不等式,求出解集即可得到a的范围.
解答:解:由已知:(x-a)?(x+a)<1,
∴(x-a)(1-x-a)<1,
即a2-a-1<x2-x.
令t=x2-x,只要a2-a-1<tmin.
t=x2-x=(x-
)2-
,当x∈R,t≥-
.
∴a2-a-1<-
,即4a2-4a-3<0,
解得:a∈(-
,
).
∴(x-a)(1-x-a)<1,
即a2-a-1<x2-x.
令t=x2-x,只要a2-a-1<tmin.
t=x2-x=(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴a2-a-1<-
| 1 |
| 4 |
解得:a∈(-
| 1 |
| 2 |
| 3 |
| 2 |
点评:考查学生理解新定义并会根据新定义化简求值,会求一元二次不等式的解集,掌握不等式恒成立时所取的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :x
:x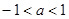 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.