题目内容
如图,四面体ABCD中,O、E分别是BD、BC的中点,
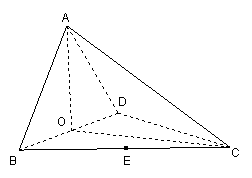
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角余弦值的大小;
(III)求点E到平面ACD的距离.
方法一: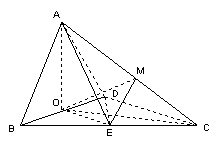 (I)证明:连结OC
(I)证明:连结OC
![]()
![]()
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]()
![]()
![]() 平面
平面![]()
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在![]() 中,
中,
![]()
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,![]()
![]()
![]() 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为![]()
(III)解:设点E到平面ACD的距离为![]()
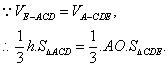
在![]() 中,
中,![]()
![]()
而![]()
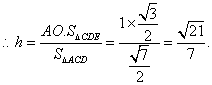
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]()
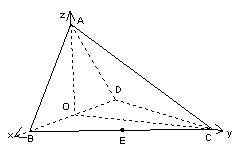
方法二: (I)同方法一.
(II)解:以O为原点,如图建立空间直角坐标系,则![]()
![]()
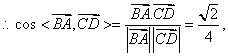
![]() 异面直线AB与CD所成角
异面直线AB与CD所成角
的大小为![]()
(III)解:设平面ACD的法向量为![]() 则
则
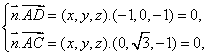
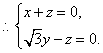
令![]() 得
得![]() 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
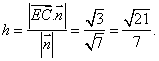

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
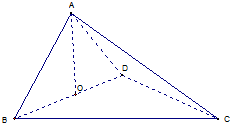 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.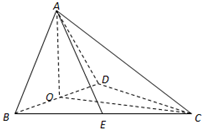 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.