题目内容
2.图1为元素周期表的另一种画法--塔式周期表,上面标有部分族及部分元素.请根据周期表中所列的元素回答问题:
(1)第一电离能最小的元素为K(填元素符号).
(2)元素Y最高价氧化物的水化物,其中心原子杂 化方式为sp3.
(3)属于过渡元素的有钪、铁(填元素名称),其中未成对电子数较少的原子,其价电子排布式为3d14s2.
(4)KY和Y3熔点分别为776℃、306℃,其原因为KCl为离子晶体,FeCl3为分子晶体.
(5)原子簇是由几个到几百个原子组成的相对独立的物质结构单元,如铝原子簇Al13、Al14.已知原子簇价电子总数为2,8,20,34,40,58…时,原子簇可稳定存在.
①铝原子簇中铝原子之间的作用力为化学键(填“化学键”、“范德华力”或“氢键”).
②Al13的稳定化合价为-1.
③Al14与周期表中所列元素Mg(填元素符号)的性质相似,其原因为Al14价电子为42,原子簇要达到稳定结构即价电子40,需要失去2个电子.
(6)NaCl的晶胞结构如图2,若将晶胞面心和体心的原子除去,顶点的Na换为U,棱心的C1换为O,得到UOn晶胞结构.已知立方晶胞参数a=415.6pm,U的相对原子质量为238.
①n=3.
②晶体的密度为$\frac{238+16×3}{(415.6×1{0}^{-10})^{3}×6.02×1{0}^{23}}$ g•cm-3(列出计算式即可).
分析 (1)根据周期表中所列元素,同主族元素原子序数越大,第一电离能越小;
(2)元素Y为Cl,最高价氧化物的水化物为HClO4,根据VSEPR理论和杂化轨道理论判断中心原子的杂化方式;
(3)Z和W分别为Sc和Fe,为过渡元素,根据电子排布式分析未成对数目;
(4)KY和Y3熔点分别为776℃、306℃,差异较大,从晶体类型角度考虑;
(5)①原子簇是由几个到几百个原子组成的相对独立的物质结构单元,能稳定存在,据此判断铝原子簇中铝原子之间的作用力;
②根据原子簇的稳定的电子结构考虑;
③根据原子簇的稳定的电子数分析,考虑原子簇达到稳定结构需要的电子数;
(6)①立方晶胞中,面心粒子占$\frac{1}{2}$,顶点粒子占$\frac{1}{8}$,体心粒子为整个晶胞所有,棱上粒子占$\frac{1}{4}$,据此计算n的值;
②根据晶体密度公式ρ=$\frac{z{M}_{r}}{{N}_{A}V}$计算,其中z为一个晶胞的粒子数,Mr为一个粒子的相对质量,V为一个晶胞的体积.
解答 解:(1)根据周期表中所列元素,同主族元素原子序数越大,第一电离能越小,第一主族的元素在同周期元素中,第一电离能最小,则第一电离能最小的元素为K,
故答案为:K;
(2)元素Y为Cl,最高价氧化物的水化物为HClO4,根据VSEPR理论,对于ClO4-,中心Cl原子的配位原子数为BP=4,孤电子对数为LP=$\frac{7-2×4+1}{2}$=0,则价层电子对数为VP=BP+LP=4+0=4,根据杂化轨道理论,中心Cl原子为sp3杂化,
故答案为:sp3;
(3)Z和W分别为Sc和Fe,为过渡元素,Sc的价电子排布式为3d14s2,未成对电子数为1,Fe的价电子排布式为3d64s2,未成对电子数为4,则未成对电子数较少的原子为Sc,其价电子排布式为3d14s2,
故答案为:钪;铁;3d14s2;
(4)KY和Y3熔点分别为776℃、306℃,差异较大,从晶体类型角度考虑,KCl为离子晶体,Cl3为分子晶体,离子晶体的熔点高于分子晶体,
故答案为:KCl为离子晶体,FeCl3为分子晶体;
(5)①原子簇是由几个到几百个原子组成的相对独立的物质结构单元,能稳定存在,据此可判断铝原子簇中铝原子之间的作用力为化学键;
②Al13的价电子数目为13×3=39,原子簇达到稳定结构,价电子数目应为40,因此需要得到一个电子达到稳定状态,则Al13的化合价为-1;
③Al14的价电子数目为14×3=42,原子簇达到稳定结构,价电子数目应为40,因此需要失去两个电子达到稳定状态,这与该周期表中所列元素X,即Mg的性质相似,
故答案为:Mg;Al14价电子为42,原子簇要达到稳定结构即价电子40,需要失去2个电子;
(6)①立方晶胞中,面心粒子占$\frac{1}{2}$,顶点粒子占$\frac{1}{8}$,体心粒子为整个晶胞所有,棱上粒子占$\frac{1}{4}$,将NaCl晶胞中面心和体心的原子除去,顶点的Na换为U,棱心的C1换为O,得到UOn晶胞结构,则一个晶胞中U的个数为$8×\frac{1}{8}$=1,O的数目为$12×\frac{1}{4}$=3,则n的值为3,
故答案为:3;
②取1mol晶胞,则含有NA个晶胞,一个晶胞的体积为V0=a3=(415.6×10-10)cm3,1mol晶胞的质量为m=(238+16×3)g,则晶体的密度为ρ=$\frac{238+16×3}{(415.6×1{0}^{-10})×6.02×1{0}^{23}}$g/cm3,
故答案为:$\frac{238+16×3}{(415.6×1{0}^{-10})^{3}×6.02×1{0}^{23}}$.
点评 本题考查物质结构综合知识,结合了塔式元素周期表考查,包含第一电离能,价层电子对互斥理论,杂化轨道理论,晶胞计算,晶体类型的判断,均为高频考点,试题有助于培养综合分析能力,需要有一定的基础,题目难度中等.

| A. | 由“C(s,石墨)→C(s,金刚石)△H=+119kJ•mol-1”可知金刚石比石墨稳定 | |
| B. | 在101kPa时,2gH2完全燃烧生成液态水,放出285.8kJ热量,则氢气燃烧的热化学方程式表示为:2H2(g)+O2(g)=2H2O (1)△H=-285.8kJ•mol-1 | |
| C. | 在101kPa时,1mol碳燃烧所放出的热量为碳的燃烧热 | |
| D. | 等量的磷蒸气和磷固体分别完全燃烧,前者放出的热量多 |
| A. | 在无色溶液中:NH4+、Fe2+、SO42-、CO32- | |
| B. | 在含大量Ba2+溶液中:NH4+、Na+、Cl-、OH- | |
| C. | 在强碱性溶液中:Na+、K+、SO42-、HCO3- | |
| D. | 在强酸性溶液中:K+、Fe2+、Cl-、SO42- |
| A. | 0.1 mol/L的HCl与0.1 mol/L的NH3•H2O等体积混合,溶液中的c(NH4+)>c(Cl-) | |
| B. | pH=3的HCl与pH=11的氨水等体积混合,溶液中的c(OH-)>c(H+) | |
| C. | pH=11的NaCN溶液中,由水电离出来的c(OH-)=c(H+) | |
| D. | CO2、SO2的水溶液能导电,但它们是非电解质 |
| A. | 分液时,分液漏斗下层液体从下口放出,上层液体从上口倒出 | |
| B. | 蒸馏时,应使温度计水银球靠近蒸馏烧瓶支管口 | |
| C. | 蒸发结晶时应将溶液蒸干,得到晶体 | |
| D. | 称量时,称量物置于托盘天平的左盘,砝码放在托盘天平的右盘中 |
| A. | 钠和冷水反应:2Na+2H2O═2Na++2OH-+H2↑ | |
| B. | AlCl3溶液中加入足量的氨水:Al3++4OH-═AlO2-+2H2O | |
| C. | 将氯气通入水中:Cl2+H2O=Cl-+HClO+H+ | |
| D. | 向Fe(NO3)2溶液中加入稀盐酸:3Fe2++4H++NO3-═3Fe3++NO↑+2H2O |
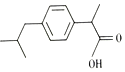
| A. | 布洛芬属于苯的同系物 | B. | 能与NaOH溶液反应 | ||
| C. | 所有原子在同一平面上 | D. | 能使溴的四氯化碳溶液褪色 |

 .
.