题目内容
【题目】如图所示，在光滑地面上静止地放置着两根质量均为
，长度均为
的匀质细杆，其中一杆由相等的两段构成，中间用光滑的铰链连接起来，两段在连接点可以弯折但不能分离.在两杆的一端，各施以相同的垂直于杆的水平冲量
.试求两杆所获动能之比.
【答案】
【解析】
本题的求解方向是通过质心的动量定理与刚体的角动量定理，求得杆的质心速度及绕质心的角速度，进而求出杆由于这两个速度所具有的动能.
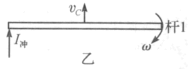
如图乙所示，设杆1在冲量
作用下，质心获得的速度为
，杆的角速度为
，由质心的动量定理，得
，由刚体的角动量原理，得
。
则杆1的动能为
.
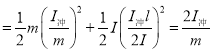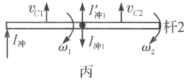
图丙所示为杆2左、右两段的受力情况，当在杆2左端作用冲量时，在两段连接处，有一对相互作用的冲量
与
，它们大小相等，方向相反.由于两段受力情况不同，各段的质心速度及角速度均不同，但在连接处，注意到“不分离”的条件，左段的右端与右段的左端具有相同的速度，现对两段分别运用动量定理和角动量定理.
对杆2左段，有
，
.①
对杆2右段，有
，
.②
由连接处“不分离”条件得左右两段的速度与角速度的关系是
.③
由①②两方程组及③式可得
，
，
于是可计算杆2的动能为
.
易得1、2两杆的动能之比.
受力分析、过程与状态分析是我们解答试题时永远不可避免的过程.
对于第一种情况，一般都能作出正确处理，但对于第二种情况，对于铰接处的作用状态并不能好好把握，很多同学错误地认为铰接处的作用是沿杆方向的，或者沿杆的方向上存在一不为零的分量，从而出错.
本题求解中，一旦破解杆2左、右两段连接处的受力及速度关系，则全盘皆活.
练习册系列答案
相关题目
