题目内容
【题目】光滑的水平面上有两块完全相同的质量均为
的平板
、
，板以匀速
向右运动，板上放着一个匀质圆柱薄筒，半径为
，质量也是，薄筒与两板间的摩擦因数均为
，薄筒和最初处于静止状态，且接触点离板左端的距离为，如图所示.
某瞬间，、两板发生完全非弹性碰撞，问：自碰撞时算起，经多长时间圆柱开始在板上做纯滚动？
【答案】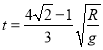
【解析】
（i）首先处理
、
发生完全非弹性碰撞的过程.
设碰后的共同速度
，则
.
（ii）薄筒在平板上的滚动阶段.
选择、共同运动的动参考系来观察滚筒在板上的运动，圆筒在动参考系中的动力学方程为（向左为正）
，
.（*）
、在此参考系下的动力学方程为
，
，所以
.
分别讨论圆筒的平动与转动.
先讨论平动，有
.
由此可得
..
再讨论转动，有
..
由此可得
.
利用纯滚动条件：
，即
，
解得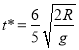
.
检查一下这个
是否是所要求的
.
前面讨论的有关过程显示，只要圆筒仍在板上，其结果就应该是正确的，所以检查的方法是看圆筒到达、界面的时间是否小于.
利用
可得圆筒在板上运动的时间
满足
，
解得（取小的值）
.
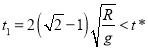这说明时刻薄筒已经抵达板，前面的方程已经不成立了，所以，不是所求的解，需要讨论圆筒进入到板后的运动情况.
先求出进入板时刻的速度与角速度分别为
，
.
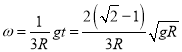再写出相应的动力学方程：
，，所以
.
再结合圆筒在板上的平动及转动方程，即前面的（*）两式，可得
，
.
利用纯滚动条件：，
即
，
代入相关数据可得
.
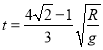本题是一道多对象与多过程的问题，其给出的解答显然遵循了程序法的解题步骤，一步一步地求解.
当然，本题的解答方法也并非没有瑕疵，敏感的答题者一开始就会意识到命题人会设置滚筒滑上平板后才会出现纯滚动，直接绕过了的求解，达到节省时间的目的.
在现有的学习背景下，任何学习者都可能无法绕开学习过程中既要追求做对，还要尽快地完成解答、节省解题时间这一应试要求.因此，我们在学习过程中，还必须熟悉一般的命题心理，为快捷的解答提供合理选择方法的依据.
名校课堂系列答案
