题目内容
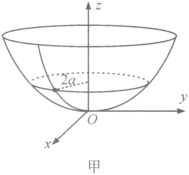
【题目】有一内壁光滑的旋转抛物面，方程
，内壁上有一质量为
的小球在一水平面内做半径为
的无摩擦的圆周运动，如图甲所示.突然，小球受到一个沿子午线方向的一个冲量，使其得到沿子午线方向的速度分量
，试证明：小球在此后的运动中，将被限制在两个水平面间运动.
【答案】证明见解析
【解析】
小球在曲面上运动，是一种二维运动，应有两个动力学方程给出描述，如果有守恒方程，则可以代替动力学方程.
本系统的守恒方程有两个.
（i）因为小球在运动过程中，受两个力作用：重力和曲面支持力，前者平行于
轴，后者通过轴，所以，对轴的力矩为零，另外，还受一个沿子午线方向的冲量，但相对于轴的冲量矩为零.
系统在受冲量前后，相对于轴的角动量守恒，其守恒量的大小为
，式中
待定.
（ii）在小球受到冲击后，除了重力（保守力）外，非保守力（支持力）不做功，所以，系统在受冲击后机械能守恒，守恒量的大小为
初始位置：
，且
，所以
.
为了明确守恒量的大小，我们先计算的值.
改写旋转抛物面方程：.
令
，
则
.
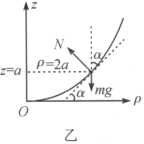
最初，
，小球受力如图乙所示，由牛顿第二定律可得
，
，
所以，
.
这里
正好是小球所在处
曲线的斜率.由得
，
，
所以，
.
则两个守恒量的大小分别为
，
.
设小球在以后运动中的任一状态的速度为
，
则
，
.
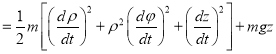利用①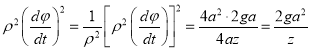
，②子午线方向的速度分量
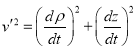可得
.
当
时，正好是小球达到最低或最高位置，由此解出的值就是最低、最高的两个平面，小球以后将在这两个平面内运动.在上式中令，有
，
整理可得
，
解得
，
.
以后小球就在这两个平面之间运动.
本题是考查角动量守恒与机械能守恒运用的代表模型.
与本题类似的曲面还有锥面、球面以及其他曲线所给出的旋转曲面等，其处理方式基本上与本题如出一辙，只是涉及的曲线不同而已.
质点在这类曲面中的运动一般有两种可供研究的运动模型，一是质点在某一高度处做稳定的匀速圆周运动，如本题中的初态；二是质点在某个高度区间内做运动，其过程遵循角动量与机械能守恒，我们即使是从定性的角度也能判断质点在最高处与最低处时，其竖直方向上的速度为零.
