题目内容
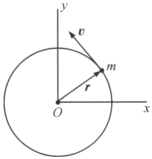
【题目】如图所示，质量为
的质点以速率
绕半径为
的圆轨道做匀速率运动.求此质点相对于圆心
点的角动量.
【答案】
【解析】
质点做圆周运动时，其速度
处处与位置矢量
垂直，
和
之间的夹角
，因此，根据角动量的定义式
，其大小
，由右手螺旋法则确定角动量
的方向垂直于圆平面向外.
设质点的角速度大小为
，因
，所以上式也可写作
.
如果写作矢量式，则有.
式中
是角速度矢量，其方向与质点的绕向之间遵从右手螺旋法则，即垂直于圆平面向外，与
的方向一致.
若取
轴沿着的方向，则质点对于轴的角动量即为
，是质点绕轴的角速度，
称为质点绕轴转动时的转动惯量.可见，质点绕轴转动时，它（对于该轴线）的角动量等于质点的转动惯量与角速度的乘积.
角速度的矢量属性在中学常规教学过程中是回避的，而角动量在中学常规教学中也不涉及，但这一内容却是竞赛的基础内容之一.
本题只是角动量这一知识点的基本练习试题，旨在掌握角动量的计算及矢量属性
练习册系列答案
相关题目
