题目内容
【题目】三个质量都为
的小球，
和
小球分别固定于一刚性轻质（其质量可忽略不计）细杆两端，并置于光滑水平面上，
小球以速度
与小球对心弹性碰撞，
与方向的夹角为45°.碰撞后，求：
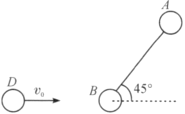
（1）杆的角速度.
（2）小球损失的动能.
【答案】（1）
（2）
【解析】
取
球与
球为系统，碰撞前后系统动量守恒，对
质心角动量守恒，同时动能守恒，由三个守恒定律即可求杆绕质心转动的角速度，而小球碰撞前后的速度也可求出，从而求出
损失的动能.
（1）由、、这3个小球组成的系统，在碰撞过程中系统的动量、角动量和能量都守恒.和对心碰撞，设其碰后速度为
，显然和
在同一直线上，同时设碰后，质心速度为
，转动角速度为
，杆长为
，由角动量守恒（对质心
），有
.
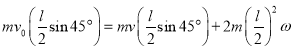由能量守恒有
.
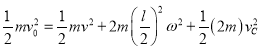由动量守恒有
.
化简以上三式得
，
，
.
由此可得
，
，
即可得.
（2）小球损失的动能为
.
本题与上一题虽然模型不同，但若比较一下两题的解答过程，不难发现它们运用的规律完全一样，都是三个守恒定律的运用.
值得注意的是，为了考查上述规律的运用情况，模型与过程也许会变得更为复杂，但无非是冲撞或被撞的球的数量增加，或者是后续过程的增加.对于这种变化，只要依据动量、能量、角动量三者之间的关系，认真处理最初碰撞产生的效果，也就不难处理了.
我们所选的这两道练习题中的能量也都是守恒的，但不排除命题人设置碰撞中动能不守恒的情况，而动量与角动量在碰撞中则应该始终是守恒的，审题时要注意到这一点.
练习册系列答案
导学教程高中新课标系列答案
相关题目
