Question

【题目】如图所示，一个质量为，半径为的均匀圆盘在光滑水平面内以速度沿方向平动，圆盘中心至轴的垂直距离为.圆盘与另一静止的、其中心位于坐标原点的均匀圆盘相碰.圆盘的质量与相同，半径为.假定碰撞后两圆盘接触处的切向速度分量（垂直于连心线方向的速度）相等，并假设碰撞前后两盘沿连心线方向的相对速度大小不变.在发生碰撞的情况下，试求：

（1）碰后两圆盘质心速度的分量和分量，结果要以给定的参量、、、和表示；

（2）碰后两圆盘的动能，结果要以给定的参量、、、和表示.

Answer 1

【答案】（1）；.

其中，.

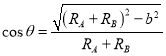（2），.

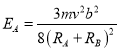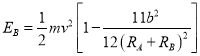【解析】

（1）如图乙所示，设碰撞时两圆盘质心连线与轴成角，由几何关系可知，对系统，在法向与切向动量均守恒，即

，①

.②

式中，、、、是、盘碰撞后沿切向与径向的质心速度，系统对点的动量矩守恒，即

.③

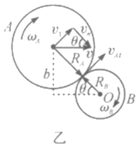
该式中，，，、为两盘碰撞后的角速度.

注意碰撞后盘既有转动又有平动，对点的动量矩由两部分组成，而盘质心在点，故角动量仅为

.

根据两盘接触处切向速度相同，有

.④

根据两盘法向相对速度不变，有

.⑤

对盘，由动量定理和动量矩原理，摩擦力的作用是

,.

即有.⑥

由上述六个方程解得

，；

，；

，.

两盘碰后质心速度的分量为

；

.

两盘碰后质心速度的分量为

；

.

其中，.

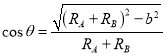（2）各圆盘的动能，是各盘质心平动动能与圆盘转动动能之和，由此可得

，

.

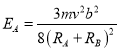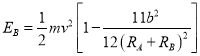本题中碰撞的是盘而不是通常情况下的球，这种模型的变化并不代表适用规律的变化.

本题情景简言之，是质量相同的运动圆盘与静止圆盘在水平面上发生非弹性斜碰.碰撞前后，质心动量守恒——系统不受外力；对点的角动量守恒——外力冲量矩为零；动能不守恒——碰撞后两圆盘接触处的切向速度分量相等，必有摩擦力存在，动能有损失.

本题给出诸多的附加条件，除了根据动量守恒与角动量守恒列出基本方程外，还须根据附加条件给出足够的补充方程，并适当选用速度分量，方可最终得解.

同学们应该注意到，只要在碰撞中不满足动能守恒，必然会出现相应的附加条件，这时附加条件便是用作方程补充的，从而完成求解.