Question

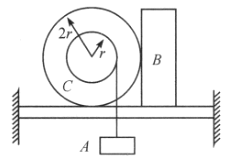
【题目】两个粒子质量均为m，电量均为q，但带异种电荷，放在均匀磁场中。磁场的磁感强度为B，方向垂直于两个粒子连线段R。它们的初速度为零，求两个粒子最靠近时它们之间的距离。磁场的磁感强度足以预先防止碰撞。

Answer 1

【答案】

【解析】

设x轴沿连接两个粒子的直线。沿_x轴在库仑引力作用下粒子加速。粒子动能的增加由其电势能的减小来决定：

。

由此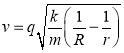。 ①

洛仑兹力垂直于速度方向且改变速度方向。粒子在y轴上的分加速度由洛仑兹力对应分力决定：

，即，

上式可改写为。

分速度的变化与两粒子之间缩短的距离关系成正比。对于最后增量进行如下计算。如果在情况下，两粒子成功沿与y轴平行方向飞出，那么它们就不会碰撞。满足这个条件的最后增量为

及。

于是。 ②

由①式和②式得到两粒子靠近的最短距离r与初始距离R及磁感强度之间的关系：

。

化简后得到二次方程：。

由此。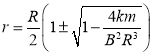

为预先防止两粒子碰撞，磁感强度值决定取正根。同时对于r要取大根，因为达到这个靠近的最短距离时，两粒子已满足。最终得到

。