Question

【题目】如图甲所示，在坐标面的原点O处有一带电粒子发射源，发射出的粒子相同，质量为m，电量，粒子出射的速率同为v，出射方向与x轴的夹角在范围内。略去粒子间的相互作用，试设计一个磁场，使得这些粒子通过磁场力的作用，成为宽度为D且沿x轴方向行进的平行粒子束。

Answer 1

【答案】边界线的显式方程：。要求,。

【解析】

可供设计选择的磁场并不唯一，为尽可能简单，取匀强磁场。

为使带正电粒子最终朝x轴方向运动，B的方向应垂直于xOy平面朝外，带电粒子从O点射出后，在磁场区域做匀速圆周运动，圆半径为

。

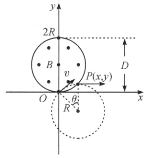
若平面上处处都有磁场，粒子将在各自圆轨道上持续运动，不可能沿x轴射出。参考图乙，为使粒子能从圆运动转变为沿x轴的直线运动，应让粒子在圆P点沿圆的切线方向射出。这意味着P点的左侧有磁场，P点的右侧没有磁场，或者说P点即为所设计磁场的边界点。P点坐标x，y由角确定如下：

，。

不同的角对应不同的，这些P点构成磁场边界线，上述两式即是磁场边界线的参量方程。消去参量，即可得边界线的显式方程：

。

这是一个圆心在y轴、半径也为R的圆，已在图乙中示出，为使粒子束出射宽度为D，要求。

与前面给出的R和B的关系式联立，即得。

需要指出，上面所得的边界方程其实给出的是由出射点组成的磁场右半圆边界线，这部分曲线必须严格界定，磁场既不能向外扩展，也不可向内收缩，磁场的左半圆边界并非由粒子出射点构成，它是为保证从O点射出的发射角在范围的粒子能做圆周运动而设定的，这部分曲线可允许向外延伸，但不可向内收缩，或者说磁场可向外扩展，但不可向内收缩。